다중 UAV의 표적 추적을 위한 협력 제어

본 논문에서 고려하는 UAV의 운동 방정식은 다음과 같고 항공기의 고도는 일정하다고 가정하였다. 따라서 항공기는 평면 내에서의 움직이며 질점 모델은 기수각(heading angle)에 영향을 미치는 롤 각(roll angle)에 의해 진행된다.

(x_i,y_i)는 평면에서의 항공기의 위치, v_i는 항공기의 속도, ψ_i는 항공기의 기수각, φ_i는 항공기의 롤 각, 그리고 g는 중력가속도를 나타낸다. 여기서 아래첨자 i는 각 항공기의 식별 번호를 의미한다. 이동하는 표적의 운동은 식 (2)의 운동 방정식으로 표현된다.

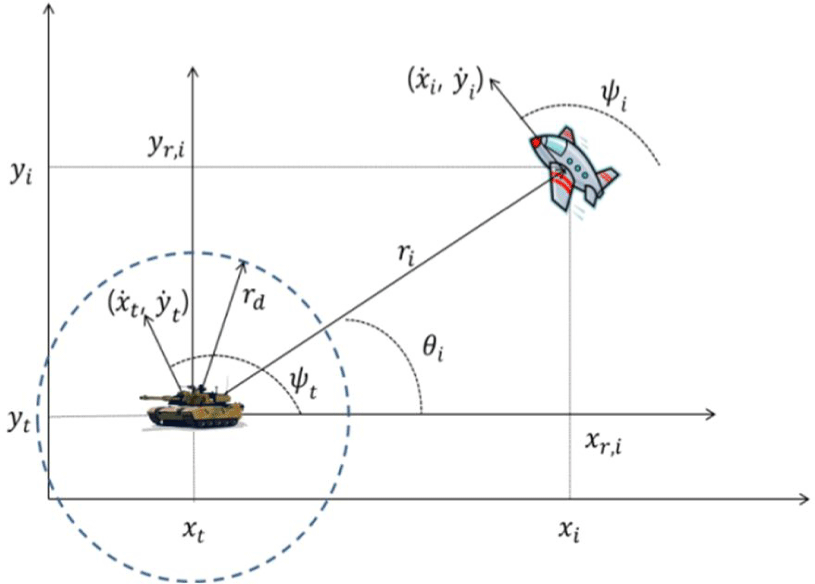
(x_t,y_t)는 평면에서의 표적의 위치, v_t는 표적의 속도, ψ_t는 표적의 기수각을 나타낸다. Fig. 1은 관성 기준 좌표계에서 항공기와 표적 간의 관계를 나타낸다. 항공기와 표적 간의 상대 거리는 식 (3) 방정식으로 표현된다.

Fig. 1. Position of the aircraft and target in a plane

Download Original Figure

(x_r,i,y_r,i)는 표적을 기준으로 한 항공기의 상대 위치이며, r_i는 항공기와 표적 간의 수평 거리이다. 여기서, r_i는 항상 측정 가능하다고 가정한다.

Lyapunov 함수를 다음과 같이 정의하며, 이 함수는 항공기가 이동하는 표적을 추적하고, 표적과 일정한 거리를 유지할 수 있게 한다.

r_d는 표적으로부터 원하는 위치이며 식 (4)를 미분하면

식 (5)와 같으며 ${\dot{x}}_{r,i}$ 와 ${\dot{y}}_{r,i}$를 식 (6)과 같이 정의하자.

그러면

${\dot{x}}_{r,i}$와 ${\dot{y}}_{r,i}$는 각각 x방향과 y방향의 상대속도이다(Eq. 7). 그러면 ${\dot{x}}_{r,i}$와 ${\dot{y}}_{r,i}$를 극좌표계로 표시해보면 식 (8)과 같다.

항공기가 표적에 접근할 때, r_i는 r_d로 수렴하므로 위의 식에서 $\dot{r}$은 0이 되고 $\dot{\theta }$는 $-\frac{v_i}{r_d}$ 가 되며 결과적으로 균일한 원운동을 하게 된다. 위에서 Lyapunov 함수를 미분한 식에 정의했던 ${\dot{x}}_{r,i}$와 ${\dot{y}}_{r,i}$를 대입하면 식 (9)와 같이 ${\dot{V}}_{D,i}$가 0 이하로 떨어지기 때문에 Lyapunov 함수는 안정적이라고 할 수 있다.

또한 정의했던 ${\dot{x}}_{r,i}$와 ${\dot{y}}_{r,i}$는 항공기의 속도 벡터라고 할 수 있으며, 원하는 기수각 ψ_d,i은 식(10)에 의해 계산된다.

속도를 극좌표계로 표시한 위의 식 (10)을 사용하여 항공기의 원하는 롤 각도 명령을 식 (11)과 같이 정의할 수 있다.

K_ψ는 헤딩 각도와 원하는 기수각의 차이에 대한 이득이고, ${\dot{\psi }}_{d,i}$는 원하는 기수각의 미분이다. 기수각 오차는 식 (12)와 같이 정의할 수 있다.

그러면, 원하는 롤 각과 기수각 오차식에 의해 다음의 식 (13)이 유도될 수 있으며, 이를 통해 원하는 기수각을 통해 표적을 추적할 수 있게 된다.

양의 K_ψ는 기수각 오차가 0으로 수렴하게 한다. 즉, 이것은 항공기가 원하는 기수각으로 표적을 추적한다는 의미이다. 표적을 향한 벡터장은 원하는 기수각이 표적로부터의 상대 위치 벡터에 의해 형성되기 때문이다. 그러므로 항공기가 벡터장 위를 날 때, 항공기는 r_d 반경을 가진 표적을 중심으로 하는 원을 그리며 수렴하게 될 것이다.

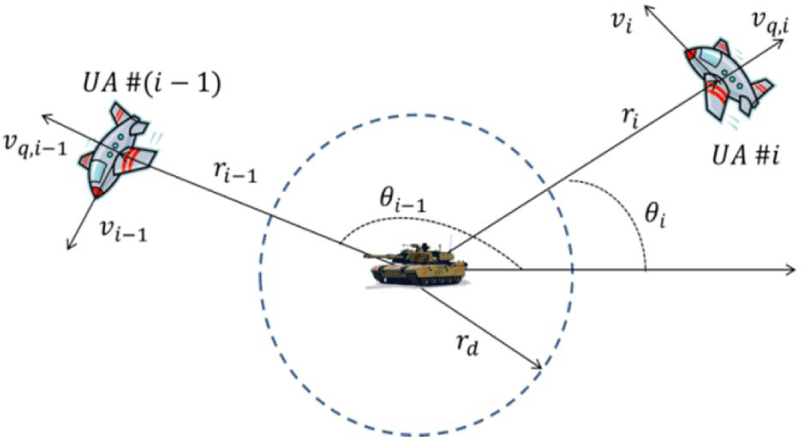
여러 항공기가 위에서 유도한 롤 각도 명령에 따라 표적을 추적할 때 위상과 거리를 제어하지 않는다면 항공기 간에 충돌할 가능성이 있다. 또한, 표적 위치와 속도의 측정 성능을 극대화하기 위해 여러 다른 관점에서 표적을 관찰할 필요가 있다. 따라서 n대의 항공기가 $\frac{2\Pi }{n}$의 위상 각도를 유지한다면 항공기 간의 충돌을 방지하고 여러 다른 측면에서 관찰할 수 있게 된다. 각 항공기의 위상 각도는 Fig. 2에 정의되어 있다.

Fig. 2. Phase angles of each aircraft with respect to the target

Download Original Figure

여러 항공기의 위상 각도를 유지하기 위해 Lyapunov 함수를 식 (14)와 같이 정의할 수 있다.

θ_i는 n번째 항공기의 위상각이고 θ_d는 항공기 사이의 원하는 위상각이다. Lyapunov 함수식을 시간에 대해 미분하면 다음 식 (15)와 같다.

한편, K_θ는 위상각 차이에 대한 이득일 때 ${\dot{\theta }}_i$를 식(16)와 같이 정의하고

이를 Lyapunov 함수식에 대입하면 ${\dot{V}}_{P,i}$가 0 또는 그 이하로 가기 때문에 안정적이라고 할 수 있다(Eq. 17).

그러면 θ_i-1과 ${\dot{\theta }}_{i-1}$에 대한 정보가 (i-1)번째 항공기로부터 받을 수 있다고 가정하자. 이는 이전에 배치된 항공기에서 수신한 위상각 및 속도 데이터를 사용할 수 있으므로 충분히 가정할 만하다. 정의했던 ${\dot{\theta }}_i$ 식에서 ${\left(\frac{r_d}{r_i}\right)}^2$ 항은 표적과의 거리가 r_d에 가까울 때 1로 수렴하게 되며, 표적과의 거리가 멀어지면 0으로 수렴하게 된다. 따라서 항공기가 표적에서 멀어지면 위상 제어 명령 대신 롤 각도 명령에 가중치를 두면 된다. 위상 제어식을 사용하여 다음과 같이 속도 제어 명령을 정의할 수 있다(Eq. 18).

결과적으로 항공기는 이 속도 제어 명령으로 원하는 기수각 식의 벡터장 방향으로 비행하게 되며, 이후 표적을 중심으로 반경이 r_d인 원으로 수렴하게 된다.

제시된 유도 제어 법칙의 성능을 검증하기 위해 6대의 항공기로 수치 시뮬레이션을 수행하였다. 표적은 5m/s 속도로 이동하고, 임무 및 안전상의 이유로 표적과의 거리는 300m를 유지했다. 표적의 위치와 속도는 모든 항공기에서 측정할 수 있다고 가정했다. 롤 각도 명령은 -45°에서 45°로 제한되었으며, 항공기의 속도는 20m/s에서 30m/s로 제한되었다. 표적과 항공기의 이동 궤적은 동일한 평면에서 동일한 고도에서 움직인다고 가정하였다.

목표의 초기 위치는 (0,0)이고, 6대 항공기의 초기 위치는 (8,001,000), (9,001,000), (10,001,000), (11,0 01,000), (12,001,000), (13,001,000)m이다. 모든 항공기의 초기 기수각은 ψ_i = 0º이며 표적은 y 방향(ψ_t = 90º)으로 5m/s로 이동한다고 가정하였다. 또한, 항공기는 표적으로부터 300m 거리를 유지하고, 동일한 위상각$\left(\frac{2\Pi }{n}={60}^{°}\right)$을 유지한다.

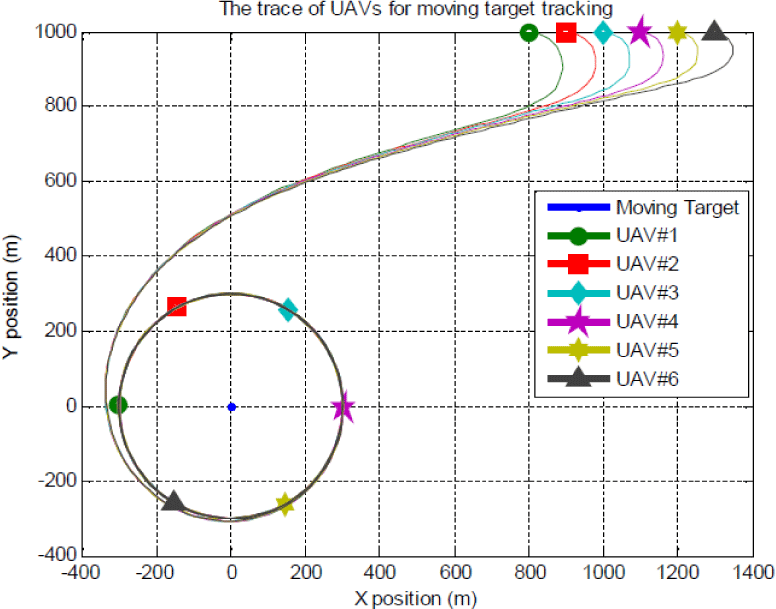
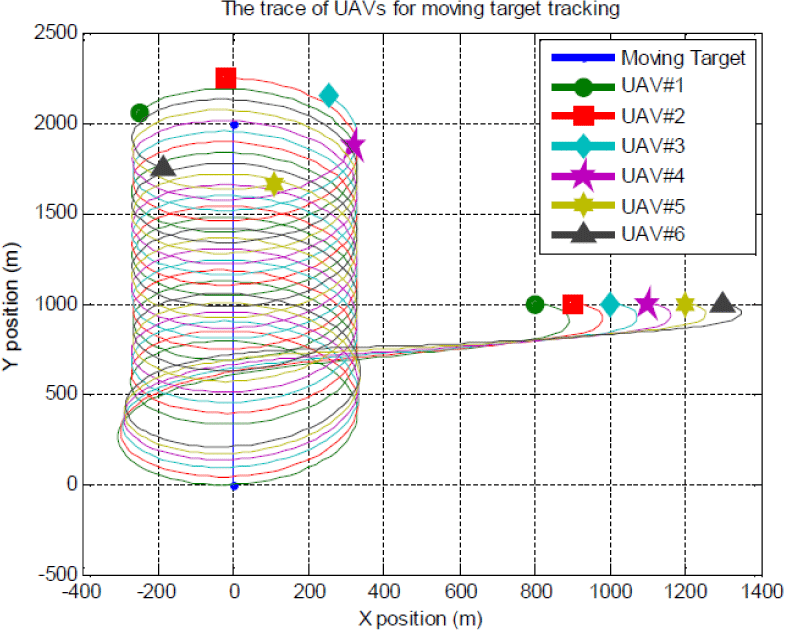
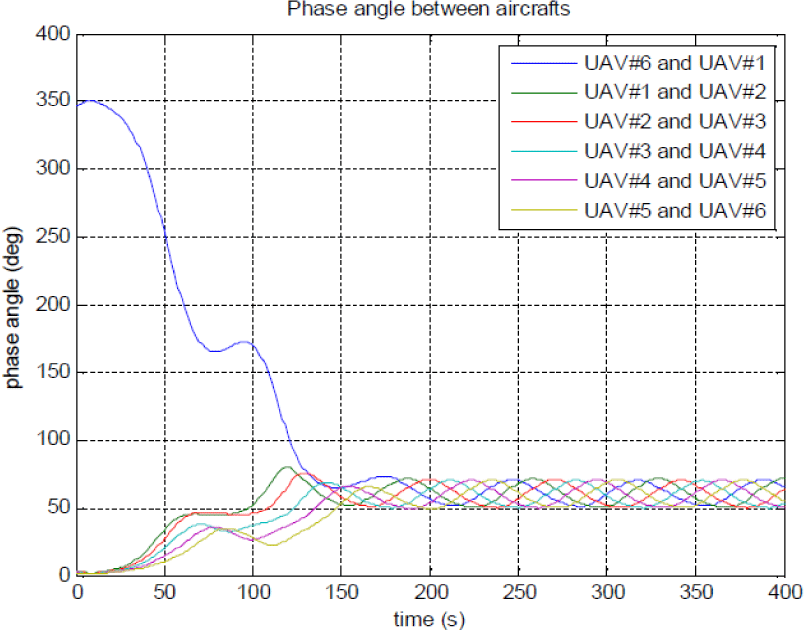
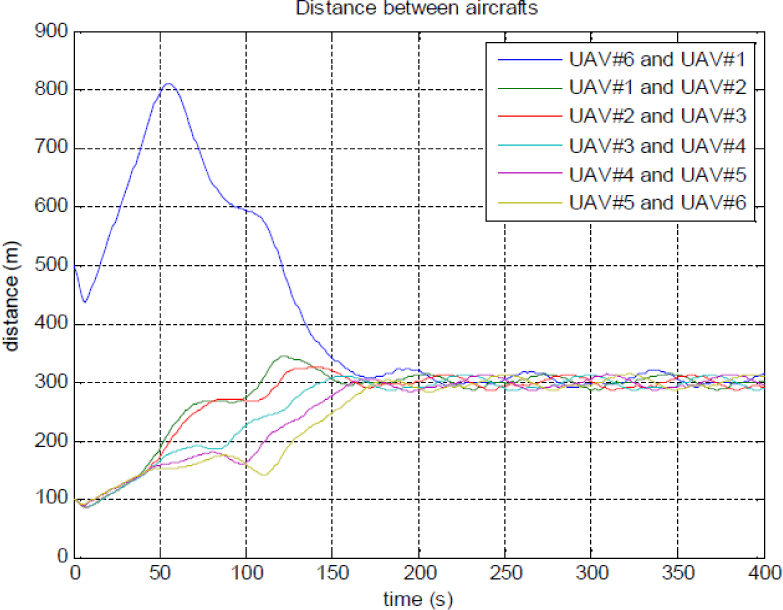
항공기의 속도는 20m/s에서 30m/s로, 롤 각도 명령은 -45도에서 45도로 제한시켰다. Fig. 3은 고정된 표적에 대한 항공기의 이동 궤적을 보여준다. Fig. 3에서 볼 수 있듯이, 모든 항공기는 표적으로부터 300m 거리를 유지하고, 그 주위를 돌고 있다. Fig. 4는 이동 표적을 추적하기 위한 항공기의 이동 궤적을 보여주고 있으며 Fig. 5는 항공기 간의 위상각을 나타내고, Fig. 6은 항공기 간의 거리를 나타낸다.

Fig. 3. Trace of UAVs for stationary target

Download Original Figure

Fig. 4. Trace of UAVs for straight moving target

Download Original Figure

Fig. 5. Phase angle between aircrafts (straight moving target)

Download Original Figure

Fig. 6. Distance between aircrafts (straight moving target)

Download Original Figure

Fig. 5에서 항공기의 위상각이 60º로 수렴하지 않지만 60±10º로 안정적으로 유지된다. 즉, 6대의 항공기가 다양한 각도에서 감시하면서 움직이는 표적을 추적할 수 있다는 뜻이다.

초기에 항공기는 같은 선상에 위치해 있었으며 즉, 모든 위상각은 0이었다. 시뮬레이션을 실행한 뒤 약 180초 후에 60±10º의 위상각으로 수렵하고 유지하게 된다. 위상각은 표적이 이동하기 때문에 주기적인 운동이 발생하였다. 이 오류를 최소화하려면 제어 이득에 대한 최적화가 필요하다.

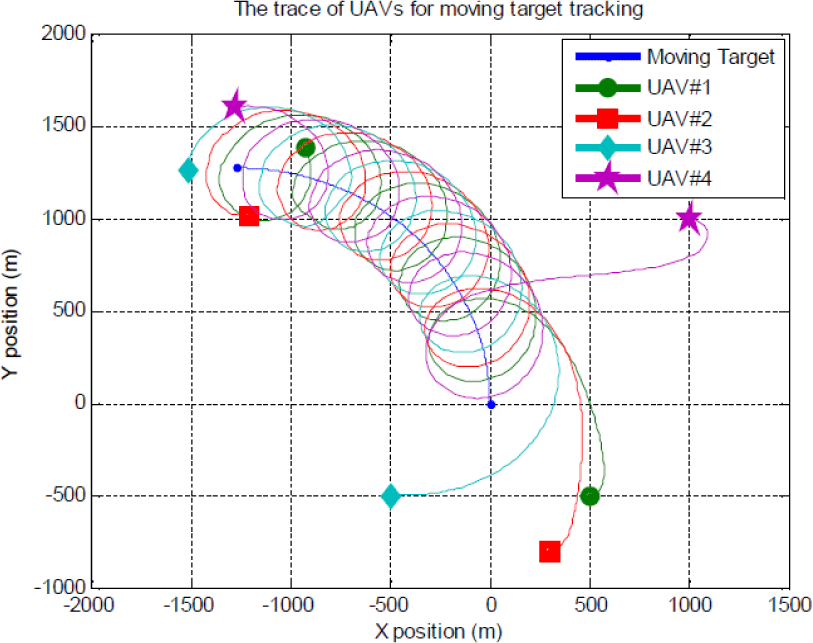
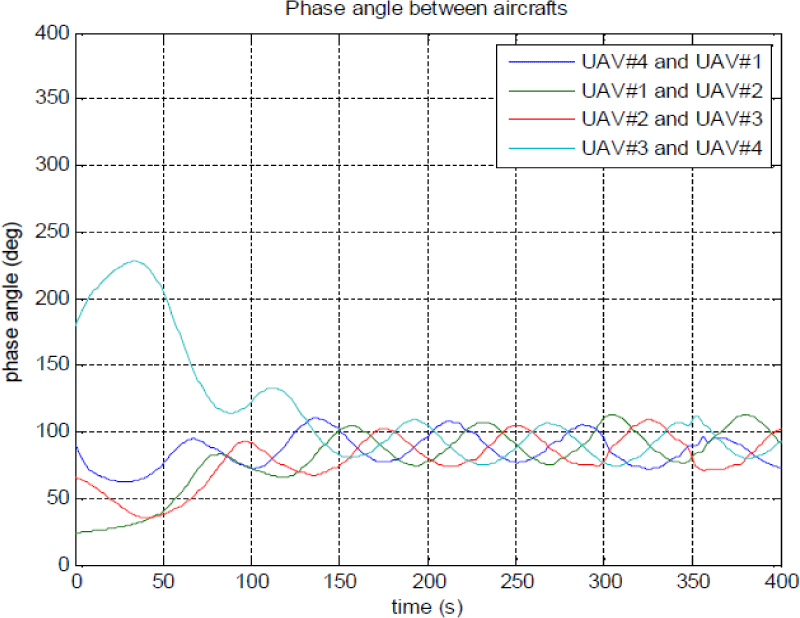
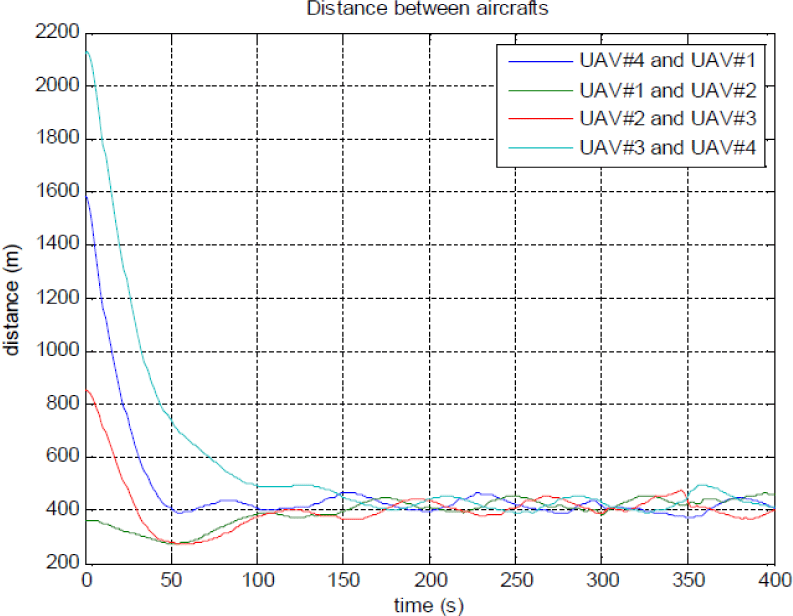
이번에는 또 다른 초기 위치와 다른 패턴의 이동을 수행하는 이동 표적에 대한 시뮬레이션을 실행해 보자. 이때 4대 항공기의 초기 위치는 (500, -500), (300, -800), (-500, -500), (1,000, 1,000)m이고 표적은 y 방향(ψ_t = 90º)으로 5m/s로 이동하며 사분원 원운동을 한다고 하자. 이때 Fig. 7과 같이 모든 항공기의 초기 위상각은 서로 다르게 세팅하였다. 그러나 약 150초 후 ±20° 주기 운동으로 $\frac{2\Pi }{n}=90°$로 수렴하고 있다. Fig. 7에서 보는 바와 같이 원으로 이동하는 이동 표적을 4대의 항공기가 원의 형태를 그리면서 잘 추적하는 궤적이 나타나고 있으며, Fig. 8과 Fig. 9는 각각 원으로 이동하는 표적을 추적하는 항공기 간의 위상각과 항공기 간의 거리를 나타내고 있다.

Fig. 7. Trace of UAVs for circle moving target

Download Original Figure

Fig. 8. Phase angle between aircrafts (circle moving target)

Download Original Figure

Fig. 9. Distance between aircrafts (circle moving target)

Download Original Figure