동축반전 로터 헬리콥터 전산유체역학 해석 및 비행시험 비교

Ⅰ. 서 론

헬리콥터의 로터와 동체 간의 공기역학적 상호 간섭은 두 구성 요소에 지속적이고 주기적인 하중 변화를 유발하여 비행 안정성과 조종성에 큰 영향을 미친다. 헬리콥터는 블레이드의 빠른 회전으로 인한 강한 와류 강도(vorticity)를 갖는 로터 주변 유동장은 제자리 비행이나 수평 비행 중에도 비정상적인 유동 특성을 갖는다. 고정익 비행기의 날개 끝에서 생성된 익단 와류(tip vortex)와 그에 따른 와류면(vortex sheet)은 날개 끝에서 빠르게 후방으로 대류되어 날개에 미치는 후류의 영향이 적지만, 헬리콥터 로터 블레이드 끝에서 발생하는 익단 와류는 뒤따라 회전하는 블레이드의 받음각에 간섭(blade vortex interaction)을 발생시킨다. 또한 헬리콥터는 전진비행(forward flight) 시 로터의 회전속도와 비행속도의 조합에 의해 전진 방향으로 회전하는 블레이드에서는 비선형적인 천음속 영역과 동적 실속이 발생할 수 있으며, 후진 방향으로 회전하는 로터의 경우 역류(reverse flow) 발생으로 인해 강한 비정상(unsteady)적인 공력 변화 특성을 나타낸다. 이러한 특성으로 인해 본질적으로 발생하는 로터 회전면의 양력 불균형을 상쇄하기 위해 로터는 플래핑(flapping) 운동을 통해 블레이드 단면의 유효 받음각을 조정하게 된다. 또한 로터 회전면의 내리 흐름(down wash)은 동체, 수평 안정판 및 테일 로터 등과도 간섭 현상을 유발하며, 고정익 항공기에 비해 상대적으로 더 뭉툭한(blunt) 헬리콥터 동체 형상 특성에 기인한 유동박리(flow separation) 현상이 복합되어 주변 유동장을 매우 복잡하게 만들게 된다.

기존에 개발된 대부분의 민군용 헬리콥터는 메인 로터(main rotor)와 테일 로터(tail rotor)로 구성된 싱글 로터(single rotor) 방식으로, 이는 상대적으로 간단한 구조로 제작이 용이한 장점이 있으나, 메인 로터 회전에 따른 각운동량(angular momentum) 보존 때문에 동체가 로터의 회전과는 반대로 돌려는 토크가 발생하여, 이를 상쇄시키기 위한 반토크(anti-torque) 발생에 필요한 테일 로터를 구동하는 데 약 5∼10% 정도의 동력이 손실되게 된다. 또한 전진익의 압축성 효과와 후퇴익의 실속으로 인한 비행 속도의 제한 및 이에 따른 로터 회전면의 양력 불균형으로 rolling moment를 발생하는 등의 단점이 있는 것으로 알려져 있다.

하나의 축에 두 개의 로터가 반대 방향으로 회전하여 토크를 상쇄하는 역할을 하는 동축반전 로터는 1859년 Henry Bright가 영국 특허청에서 최초로 특허를 획득하였다. 이 로터 구동 방식은 초기 헬리콥터 개발자들이 집중적으로 연구했지만, 복잡한 로터 계통의 신뢰성과 상대적으로 높은 유해항력의 발생 등의 문제로 당시의 기술력으로는 실용화에 어려움이 있었다. 이후 기술의 발전으로 1960년대 대잠수함 작전용으로 미국 해군이 Gyrodyne사 QH-50 DASH(Drone Anti-Submarine Helicopter) 무인 헬리콥터 750여대를 운용한 사례가 있으며, 구소련에서는 1950년대 Ka-15 개발을 시작으로 Ka-226, Ka-32 및 Ka-52 등을 생산한 러시아의 Kamov사는 유인 헬리콥터를 주로 생산하여 동축반전 헬리콥터 분야에서 유명한 기업이 되었다. 이 중 Ka-32는 러시아 해군의 대잠 작전용으로 개발된 Ka-27을 민수용으로 개량한 모델로 한국에서도 민간 항공사를 비롯해 산림청, 해양경찰 및 공군에서 약 60대를 운용 중이며, 산림청에서 운용 중인 기종의 형상은 Fig. 1과 같다.

Fig. 1. KA-32 firefighting helicopter operated in the Korea forest service

Download Original Figure

동축반전 로터 헬리콥터의 풍동시험 및 유동해석과 관련된 주요 연구 사례는 다음과 같이 요약할 수 있다. NASA의 Coleman(1997)은 1950년대부터 1990년대 중반까지 미국, 러시아, 일본, 영국, 독일에서 수행한 동축반전 로터에 대한 이론 및 풍동시험 사례를 조사하여 상/하 로터의 거리 간격과 하중 분담 비율, 후류 구조 및 블레이드 고형비(solidity) 효과 등을 전반적으로 분석하였다. 로터 형상만을 고려한 초기 풍동 시험 사례로는 제자리 비행 상태(hovering condition)에서 싱글 로터와 동축반전 로터의 공력 성능을 비교한 사례(Harrington, 1951)가 있고, 동일한 로터 모델을 이용해 전진 비행 성능을 측정한 사례도 있다(Dingeldein, 1954). 이후 동축반전 로터의 성능, 상/하 로터의 간섭 및 비틀림각에 대한 풍동시험 및 해석적 연구를 수행한 사례가 있다(MaAlister et al., 2006; MaAlister et al., 2008).

동축반전 로터 헬리콥터의 전기체 형상에 대한 연구로는 1980년대 초반 NASA에서 수행한 Sikorsky사 XH-59A 개념모델에 대한 전진 비행 풍동시험(Felker III, 1981)과 1990년대 초반 Ka-32 헬리콥터 블레이드 끝단에 내장한 연막 발생기를 이용한 비행 시험을 통해 제자리 비행 및 전진 비행 중 변화하는 로터 후류 구조를 측정한 사례가 있다(Akimov et al., 1994).

관련된 수치해석 사례로는 동축반전 로터의 공력해석을 위한 고전적인 blade element momentum theory (BEMT)의 개선 연구(Leishman et al., 2006)와 free-wake 기법을 적용한 덴덤, 틸트 및 동축반전 로터의 성능해석 및 검증(Bagai and Leishman, 1996)이 있다. 그리고 vorticity transport model (VTM) 기법을 이용한 동축반전 로터의 성능해석(Kim et al., 2006), 압축성 Navier-Stokes 방정식과 비정렬 중첩 격자계를 이용한 제자리 비행 상태 풍동시험 모델에 대한 해석(Lee, 2009), 비압축성 Navier-Stokes 방정식과 비정렬 적응격자를 이용한 제자리 및 전진 비행 상태의 풍동시험 모델에 대한 해석(Barbely, 2016) 등이 있다. 그 다음으로 동적 중첩 격자(moving overset mesh) 기법을 적용한 전산유체역학 해석기법과 효율적인 trim 해석 모델을 활용한 제자리 비행 상태 풍동시험 모델 해석비교(Qi et. al., 2019) 및 압축성 Naver-Stokes 방정식과 정렬 중첩 격자계 및 trim 해석을 적용한 전진 비행 상태 풍동시험 모델 해석(Hayami et. al., 2023) 사례 등이 있다. 그러나 기존 연구는 대부분 동축반전 로터 자체의 해석에만 집중되어 있으며, 동체의 간섭효과까지 고려한 수치해석 및 비교 사례는 드물다. 이에 본 논문에서는 회전하는 동축반전 로터와 동체 형상을 포함한 Kamov Ka-32 헬리콥터의 전기체 형상 및 진보된 전산유체역학 모델링을 수행하고, 산림청의 실제 비행시험 데이터와 비교하여 수치해석 기법의 신뢰도를 평가하였다.

Ⅱ. 전산유체역학 모델링

2.1 KA-32 헬리콥터 형상 모델링

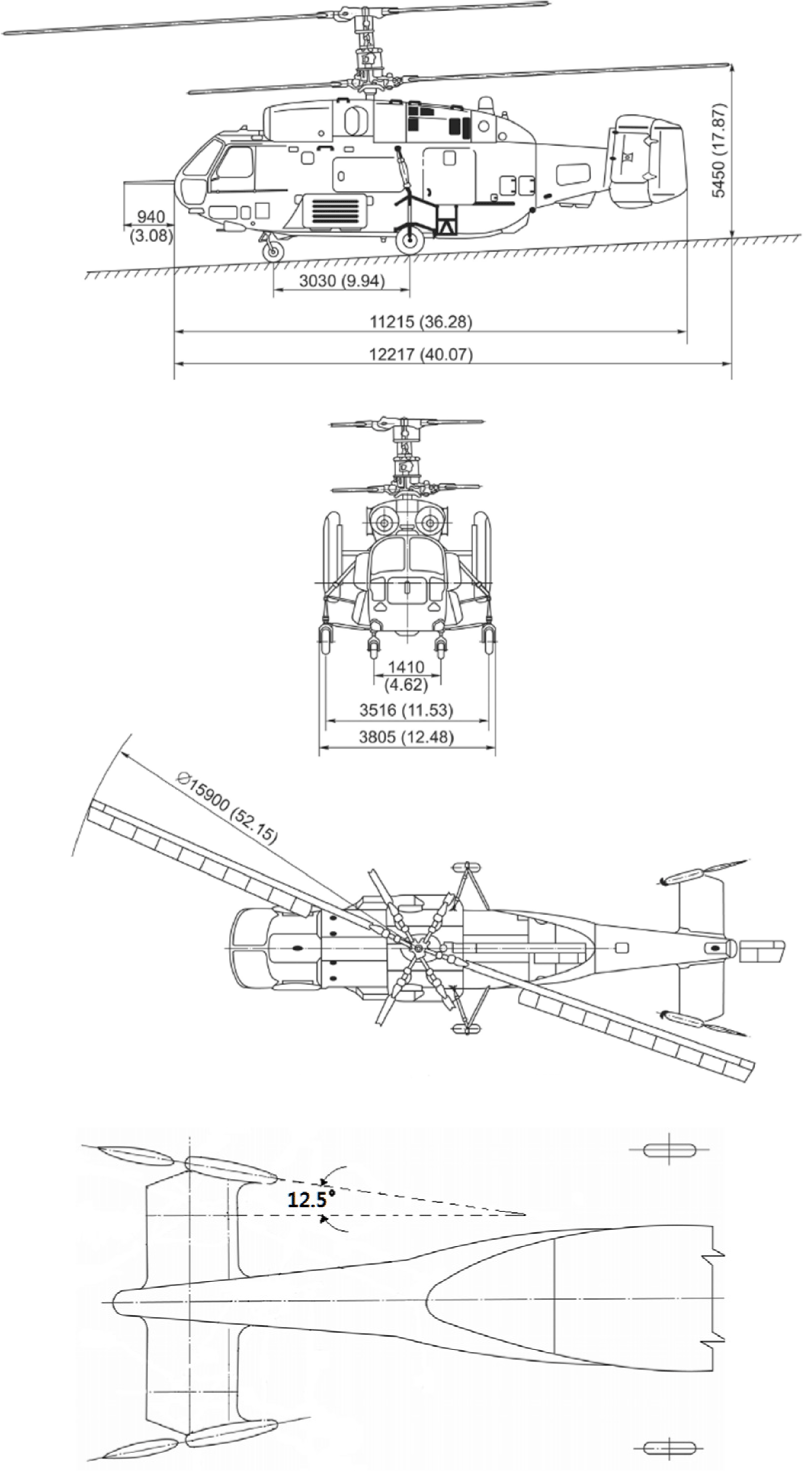
러시아 Kamov사의 KA-32 동축반전 로터 헬리콥터(Fig. 2)는 비슷한 체급의 단일 로터 헬리콥터에 비해 협소한 공간으로 운용이 가능하고 강풍에서 안정성이 우수한 기종으로 시동 제한 풍속은 약 40knot이고, 제자리 비행 제한 풍속은 약 20knot이다.

Fig. 2. Overal dimension of the Ka-32 helicopter (unit: mm (inch))

Download Original Figure

본 연구에서는 해당 기종 도입 시 제작사에서 제공한 교육 자료(Ka-32T Methodical Text Book, Kamov Company)와 기체 수리를 위해 발행된 IPC(illustrated part catalog)의 도면과 실측 데이터를 활용하여 로터 블레이드, 동체 및 하부 물탱크 형상에 대한 3차원 CAD 모델링을 직접 수행하였다.

Ka-32의 외형과 치수는 Fig. 2와 같으며, 싱글 로터 방식에 비해 상대적으로 넓은 수직 및 수평 안정판을 확인할 수 있다. 이는 동축반전 로터 헬리콥터의 전형적인 특징으로 헬리콥터 트림(trim) 자세 유지를 위해 충분한 모멘트를 제공하기 위해서 짧은 암(arm)을 보상할 수 있도록 넓은 면적이 필요하기 때문이다. Ka-32의 수평 안정판의 면적은 2.91m²이고, 동체 중심을 향해 12.5˚의 각도로 부착된 좌우 수직 안정판의 면적은 각각 3.05m²이다.

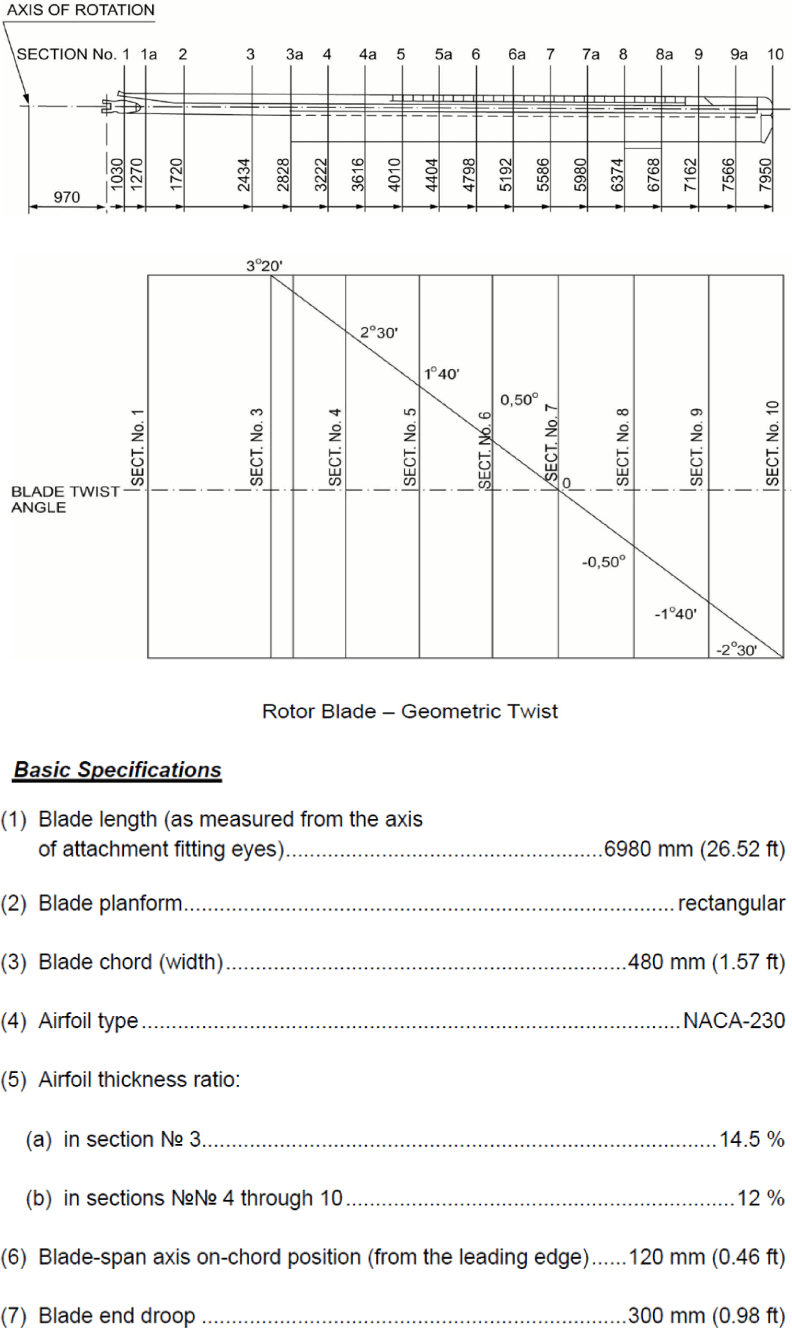
Ka-32 헬리콥터 로터 블레이드의 형상, 크기 및 제원은 Fig. 3과 같다. 회전축 중심에서 블레이드 끝단까지 7,950mm의 반지름과 초기 비틀림각을 가지며, 코드길이는 480mm로 고형비(solidity, σ)는 0.05이다. 동축반전형 로터 블레이드는 모두 6개로, 시계 방향으로 회전하는 상부 로터와 반시계 방향으로 회전하는 하부 로터에 각각 3개씩 장착되어, 약 90% 엔진출력 조건에서 평균 272rpm의 회전속도를 가진다. 상부 및 하부 로터의 간격은 1,460mm로 로터 직경 대비 9.18%이며, 로터 회전축(main rotor shaft axis)은 동체 수직축에 대해 -4.5˚ 기울기를 가지는데 전방으로 기울어져 있는 상태에 해당한다.

Fig. 3의 Section No.7의 비틀림각은 0˚이며, Section No.8에는 진동 수정 작업을 위해 익단 궤적을 조절하는, 트랙킹(tracking)을 위한 트림탭(trim tab)이 장착되어 있다. 상부 및 하부 블레이드의 익형은 상부 블레이드의 경우 Section No. 3에서 하부 블레이드의 경우는 Section No. 3a에서 시작된다. 하부 블레이드의 Section No. 3에는 진동 저감을 위한 pendulum absorber가 장착되어 있다. 본 연구의 유동해석 모델링에서는 단순화를 위해 트림탭과 pendulum absorber 형상은 고려하지 않았다.

Fig. 3. Overal dimension of the Ka-32 helicopter (unit: mm (inch))

Download Original Figure

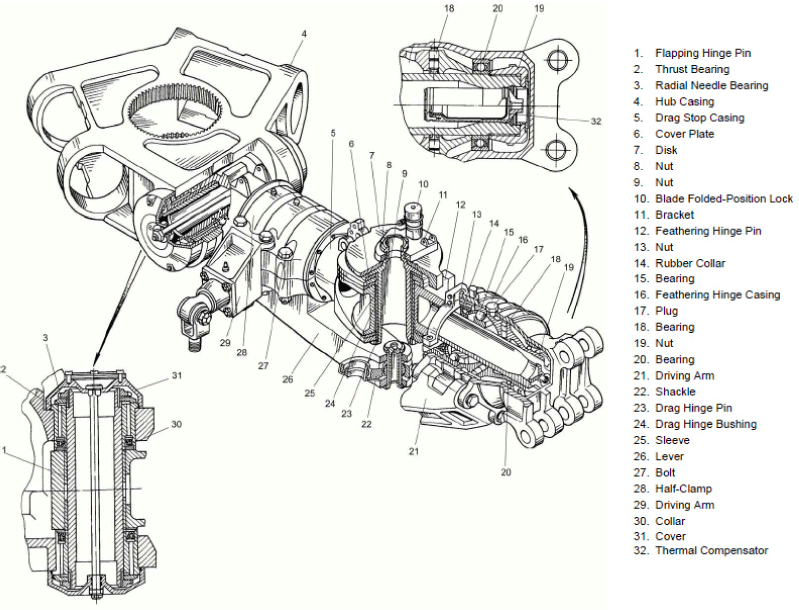
Fig. 4는 상부 로터 허브의 구성품을 나타내고 있으며, 상/하부 플래핑 힌지(flapping hinge)는 로터 중심축에서 150mm 지점에 위치하며, 최대 플래핑 각도는 20˚이다. 리드-래그(lead-lag) 힌지(drag hinge)는 로터 중심축으로 부터 565mm에 위치하여 회전 방향으로 5˚, 회전 반대 방향으로 7˚의 허용 각도를 가진다.

Fig. 4. Upper rotor hub parts of the Ka-32 helicopter (IPC, Kamov Company)

Download Original Figure

플레핑에 의한 블레이드 피치를 보상하는 δ3 각도는 36˚이며, 플래핑 각도(β)에 따른 블레이드 피치 각도의 변화(Δθ)는 △θ = -tan(δ3) · β이다. 로터 허브에 장착된 블레이드의 부착각도(setting angle)는 사이클릭 조종간이 중립에 있고 콜렉티브 조종간이 최저 위치에 있을 때 상부 블레이드는 12˚, 하부 블레이드는 10.75˚ 상태에 위치하게 된다.

2.2 운항시험 및 데이터

Ka-32 헬리콥터에 대한 로터-동체 간섭 유동해석과 비행시험 데이터 비교를 위해 조종계통과 FDR(flight data recorder) 보정을 완료하고, 산림청에서 운용 중인 기체를 대상 모델로 선정하였다. 해당 기체는 3,000 리터 용량의 물탱크(fire attack system)를 장착하여 산불 진화용으로 운용되고 있는 기종(Fig. 1)이며, 제자리 비행시험은 약 30m 고도에서 전진 비행시험은 약 120m 고도에서 수행되었으며, Fig. 5와 같이 자세 및 조종 제어와 관련된 17개 항목의 데이터를 기체에 장착된 FDR에서 추출하였다.

Fig. 5. Original time signal extracted from flight data recorder (FDR) of Ka-32 helicopter

Download Original Figure

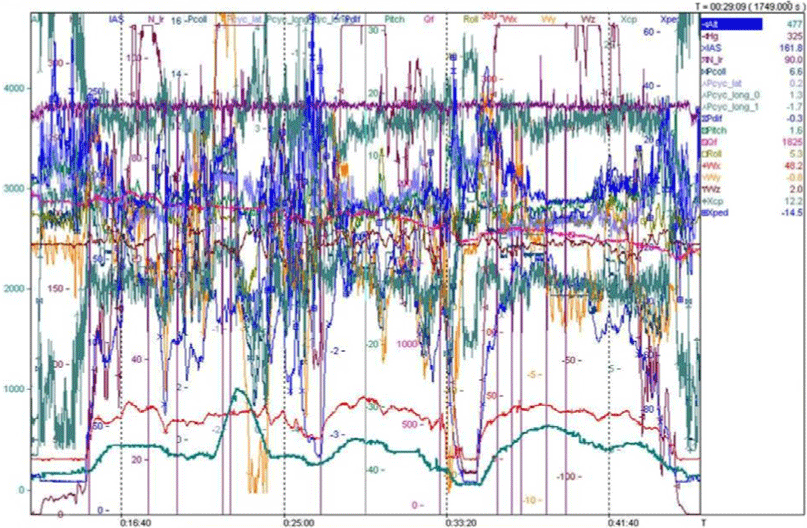
FDR에서 추출한 데이터 중 근사 제자리 비행 및 전진 비행 조건에 대한 CFD 유동해석 조건을 설정하기 위해 특정 시간 구간을 선별하여 추출하여 도시한 그래프는 Fig. 6 및 Fig. 7과 같다. 여기서 가능한 수평 구간에 대한 평균 데이터를 반영하여 Table 1과 같은 해석 조건을 선정하였다. 표에서 V_I는 indicated air speed, α_F는 동체의 피치각, A₀는 collective pitch angle, A₁은 lateral cyclic pitch angle, B₁은 longitudinal cyclic pitch angle을 의미한다. 여기서 유의할 점은 블레이드의 피치각 0˚에 해당하는 기준 위치는 회전 중심에서 블레이드 스팬방향(spanwise)으로 70.264% 지점의 Section No. 7이다(Fig. 3 참조).

Fig. 6. Selected time range of flight test data for a hovering condition of Ka-32 helicopter

Download Original Figure

Fig. 7. Selected time range of flight test data for a forward flight condition of Ka-32 helicopter

Download Original Figure

Table 1. Extracted blade motion parameters from FDR data

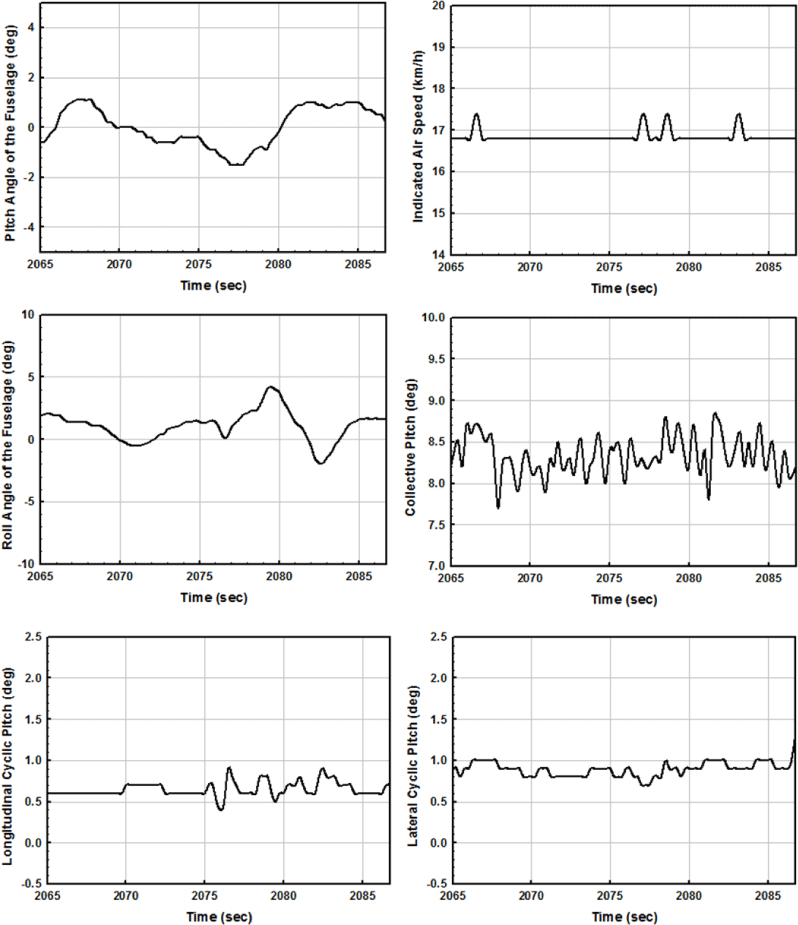
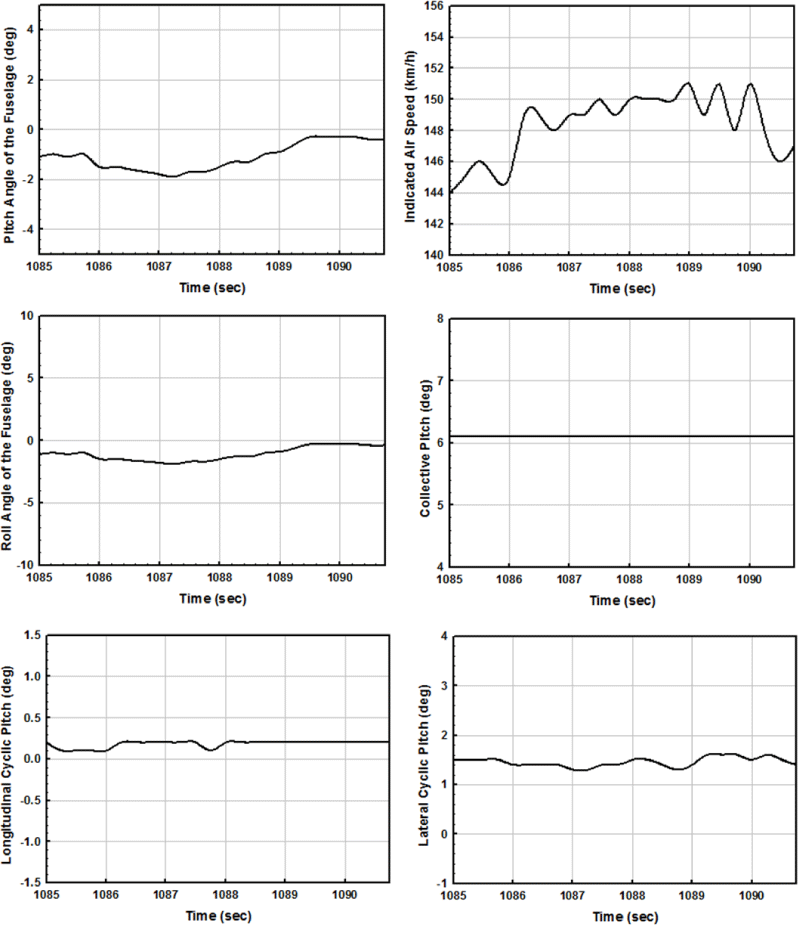
Case	VI (km/h)	αF (deg)	A0 (deg)	A1 (deg)	B1 (deg)
Hovering flight	16.8	4.5	8.3	0	0
Forward flight	148.8	-1.1	6.1	0.2	1.5

Download Excel Table

본 연구에서는 실제 헬리콥터 비행 조건과 같이 블레이드 운동을 고려할 수 있도록 동적 중첩 격자(moving overset mesh) 기반의 비정상 전산유체역학(Unsteady CFD) 유동해석을 수행하였다. 블레이드 회전 방위각(ψ)에 따른 피치각도 변화를 CFD 유동해석 모델에 구현하기 위해 아래의 식을 적용하여 개별 블레이드의 운동을 반영하였다.

$$A\left(\Psi \right)=A_0+A_1\cos \left(\psi \right)+B_1\sin \left(\psi \right)$$

(1)

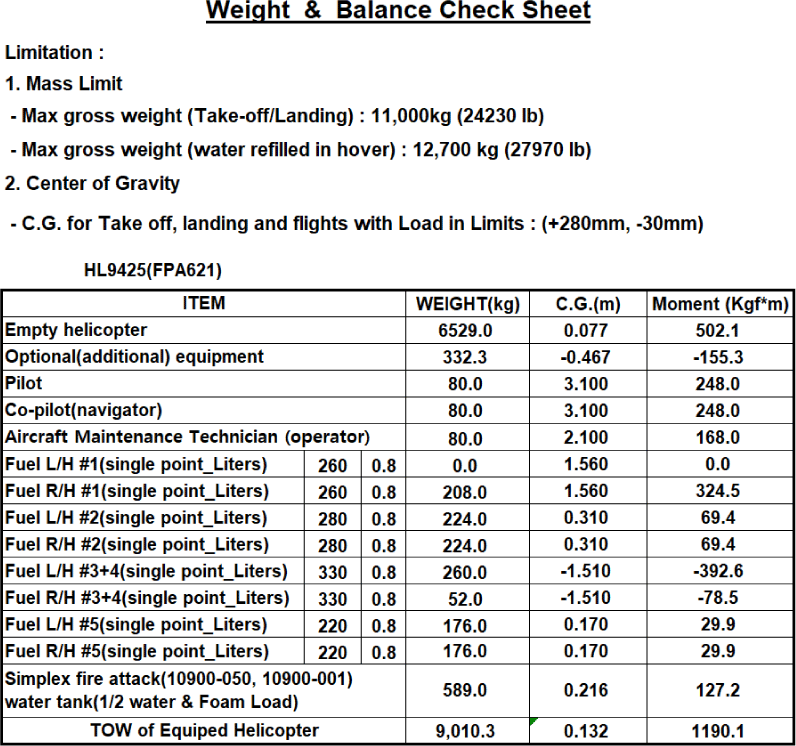
비행시험 중 발생하는 추력을 실시간으로 직접 측정하는 것이 불가능하며, 비행시험을 위해 실제 주기적으로 계측된 기체 중량과 평형(weight and balance) 정보(Fig. 8)를 기반으로 총중량과 무게 중심에 대해 역으로 계산이 가능하다. 비행시험 기체의 총중량은 9,010.3kg이며, 계산된 무게 중심은 로터 회전축에서 전방으로 132mm 지점에 위치한다. 단, 이는 산불 진화용 물탱크와 동체 측면의 소화액 탱크(foam tank)가 빈 상태의 중량 조건이다.

Fig. 8. Weight and balance check sheet

Download Original Figure

2.3 전산유체역학 해석기법

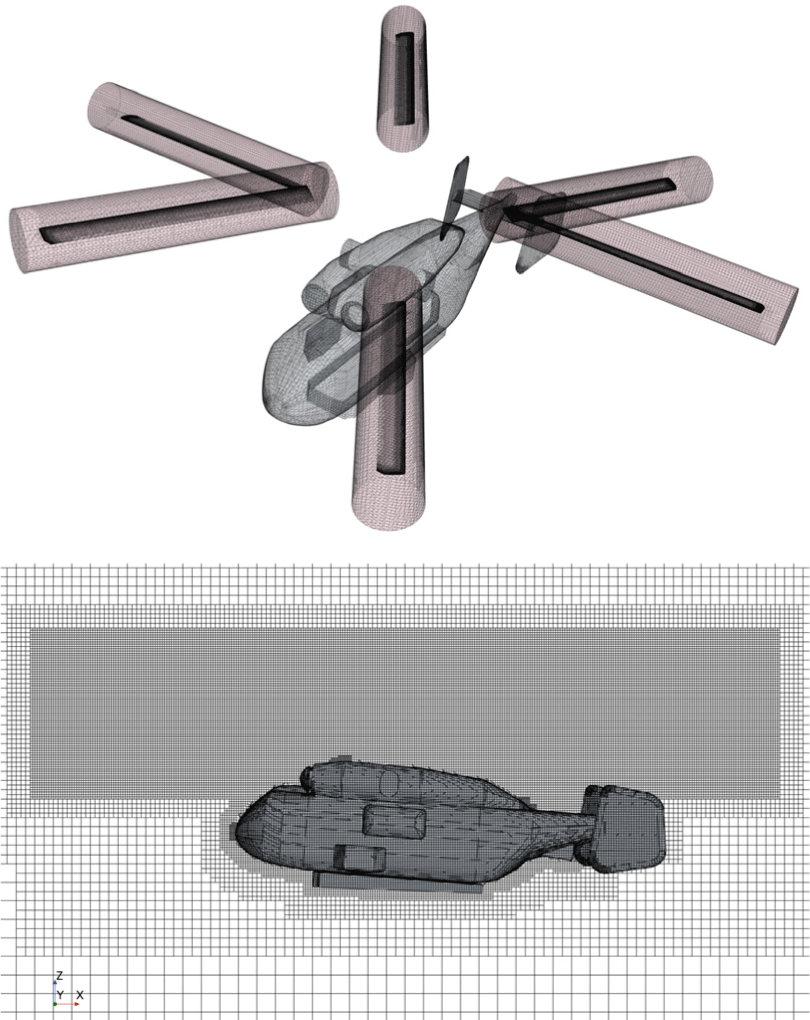
본 연구에서 전산유체역학 해석은 압축성 Navier-Stokes 방정식에 기반하였다. 유동해석 격자 생성 및 해석은 검증된 상용 전산유체역학 해석 프로그램인 STAR-CCM+ 및 모든 블레이드의 방위각에 따른 개별적인 피칭 운동을 고려하기 위한 코드를 생성하여 연동 해석하였다. 회전 및 운동하는 동축반전 블레이드와 동체 형상을 동시에 고려한 3차원 비정상 유동해석을 위해 Fig. 9와 같이 고품질의 hexahedron 요소 기반의 비정렬 중첩 격자계를 생성하여 공력해석을 수행하였다. 유동해석 격자의 총 셀(cell) 수는 블레이드 및 동체 면에 10개의 경계층 격자를 포함하여 약 1,338만 개이다. 배경(background) 격자는 약 745만 개의 셀로 구성되며, 동체 형상을 포함하고 있다. 각각의 블레이드는 방위각에 따라 변하는 운동을 반영할 수 있도록 6개의 overset 영역으로 구성되어 있으며, 하나의 overset 영역의 셀 수는 약 100만 개다. 블레이드의 경계층 격자는 평균 y+ 값이 1 부근이 되도록 사전 예비 해석을 통해 첫 번째 경계층 높이와 조밀도를 조정하는 과정을 거쳤다. 또한 모든 블레이드의 overset 영역과 배경 격자는 distance weighted 개념의 인터페이스 경계조건이 반영되었다. 각각의 개별 블레이드의 운동은 superposing motion 기법을 적용하여 Eq. 1에 기반하여 비정상 유동해석 시간 전진에 따라 실시간으로 변화하는 방위각에 대해 동적인 cyclic pitching motion이 구현될 수 있도록 field function 코드를 작성하여 반영하였다.

Fig. 9. Hexaheron mesh based unstructured overset grid for the Ka-32 helicopter

Download Original Figure

본 연구에서 비정상 점성 CFD 유동해석 기법은 실용적이면서도 정확도가 높은 모델로 잘 알려진 shear stress transport (SST) k-ω 난류 모델을 적용하였다. 비정상 CFD 해석기법의 경우, 총 해석 시간은 응답해석 시간을 시간간격(time step)으로 나눈 반복 계산 횟수에 비례하게 된다. 본 연구에서는 해석 시간을 최소화하면서 수렴된 결과를 얻을 수 있는 시간 간격 설정을 위해 시간 간격에 대한 수렴성 테스트를 다양하게 수행한 후 최적의 값을 적용하였다. 설정된 시간 간격은 블레이드 1 회전 유동 해석을 수행하는데, time-step 당 0.5˚ (Δωt=0.5 deg) 회전 조건에 해당하는 조건이다. 또한 비정상 유동해석의 각 시간 단계에서 수렴성 증진을 위한 sub-iteration은 10회를 반영하였으며, 2차 시간 이산화 기법(2nd-order time discretization method)을 적용하였다. 원방경계(far-field)는 자유흐름(free stream) 조건을 설정하였다. 비행시험이 약 120 m의 낮은 고도에서 수행되었기에 원방경계 대기압 조건은 101,325Pa을 대기 온도는 300K를 부가하였다. 그리고 근사 제자리 비행 조건의 속도는 16.8km/h (4.7m/s)를 전진 비행 조건의 속도는 148.8km/h (41.3m/s)를 반영하였다.

Ⅲ. 해석결과 및 검토

앞서 제시한 Table 1의 조건과 Fig. 9의 유동해석 격자에 대해 제자리 비행 조건과 정상 전진 비행 조건에 대한 비정상 상태 전산유체역학 해석을 수행하였다.

제자리 비행 조건에 대한 해석의 경우, 블레이드 회전속도(272rpm, 28.484rad/s)와 Table 1에 제시된 동체 자세각과 Eq. 1의 계수들을 반영하여 방위각에 따른 블레이드 피치 운동을 구현하는 별도의 코드(filed function)를 작성하여 연동한 비정상 유동해석을 수행하였다. 전술하였지만 Ka-32 헬리콥터의 로터 회전축은 동체 수직축에 대해 전방으로 -4.5° 기울어진 상태로 장착되어 있다. 따라서 제자리 비행시험 시 동체의 피치각은 Table 1과 같이 +4.5°를 가지며, CFD 해석 모델은 이를 고려하기 위해 블레이드 및 동체의 초기 CAD 형상을 y축 방향으로 +4.5° 회전시킨 상태로 유동해석 격자를 생성하였다. 그리고 제자리 비행 조건에 대한 비정상 유동해석을 위한 시간 간격은 unsteady global iteration 1회에 블레이드 방위각이 0.5˚ (Δωt=0.5deg) 회전 진행하는 조건으로 설정하였으며, 이를 물리적인 시간 간격으로 환산하면 Δt=3.0637×10^-4 sec 이며, 로터 블레이드 1회전에 필요한 비정상 유동해석 시간 전진은 720회가 필요하다. 각 시간 진전 단계에서 비정상 해의 수렴 증진을 위한 sub-iteration은 5회를 반영하였다. 제자리 비행 조건의 경우, 블레이드가 4회전 한 이후부터는 수렴된 비정상 유동해석 결과를 얻을 수 있었으나, 충분하게 수렴된 결과를 얻기 위해 총 10회전 이상을 해석하였다. 참고로 이 해석에는 AMD Ryzen Threadripper PRO 5995WX 64-core와 512 GB RAM 사양의 병렬연산 서버 2대를 활용하였으며, 5회 sub-iteration 과정과 overset 경계 데이터 교환시간을 포함하여 1회 비정상 시간 전진에 약 1분이 소요되었다. 따라서 블레이드 1회전 해석에 소요되는 수치해석 시간은 약 720분(12시간)이고, 10회전(t_max=2.21 sec) 해석에는 약 5일이 소요되게 된다.

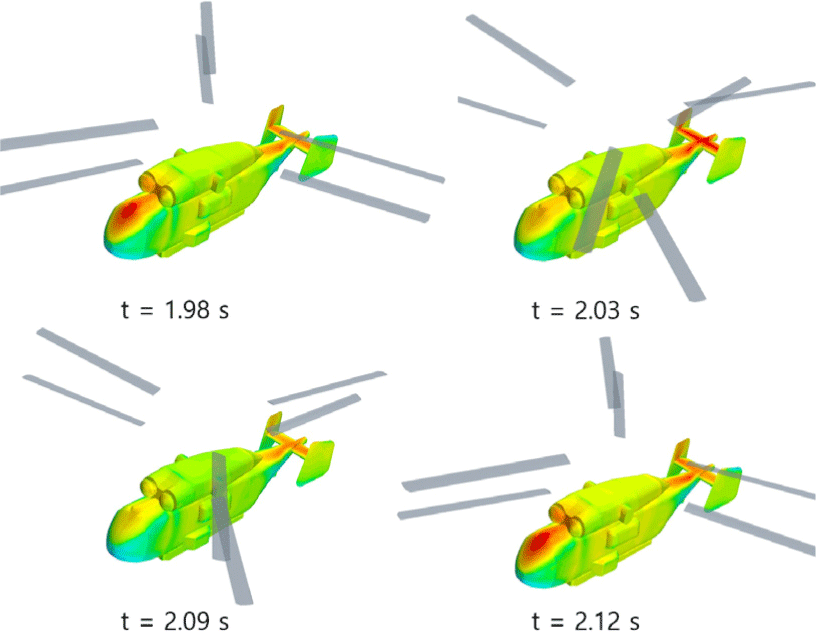
제자리 비행 시 특정 시간 순간에서 동체와 로터 주변의 와류 강도 분포를 Fig. 10에 나타내었다. 블레이드 끝단에서 발생한 vortex가 로터보다 작은 크기의 반경 궤적으로 흘러 내려가는 경향을 보이며, 비행시험 조건과 동일하게 4.7m/s를 유동해석의 원방경계 유입속도로 반영하였기 때문에 바람 방향으로도 vortex의 움직임이 약간 관찰되고 있다. 또한 동체에서 발생하는 와류도 일부 관찰되고 있으며, 와도 분포를 살펴보면 기존의 산림청에서 활용 중인 기체에 장착된 하단의 물탱크 후단에서부터 테일 붐에 장착된 도플러 센서 부근까지 발생하는 와류 강도의 수준을 확인할 수 있다. Fig. 11은 제자리 비행 시 동체 표면의 비정상 순간 압력 분포도를 보여주고 있는데, 블레이드가 동체와 근접하는 지점에서 블레이드 내리 흐름 영향으로 인해 높은 압력 상태가 유발되는 것을 볼 수 있다.

Fig. 10. Instantaneous vorticity contour on the symmetric plane of the fuselage under a hovering condition

Download Original Figure

Fig. 11. Pressure contours on the fuselage surface of the Ka-32 helicopter at different time-steps (hovering condition)

Download Original Figure

제자리 비행 시 수렴된 구간의 시간에 대한 추력 변화를 Fig. 12에 제시하였다. 블레이드 회전속도가 272rpm (28.484rad/s)이므로 1회전에 소요되는 시간은 0.221 sec이며, 상부 3개 및 하부 3개 블레이드의 교차 간섭 및 동체 간섭 영향으로 1회전 시간에 대응하는 시간 구간에서 6번의 최대 추력 변곡점이 발생함을 확인할 수 있다. 그림에서 점선은 블레이드가 발생하는 섭동 추력을 나타내며, 실선은 동체까지 포함한 전체 추력 섭동을 나타내고 있다. 이 결과를 보면 Ka-32 헬리콥터의 경우, 제자리 비행 시 블레이드와 동체의 간섭 영향으로 발생하는 평균 추력의 감소는 약 3.54% 수준임이 파악되었다. Fig. 12의 아래 그림은 각각 상부 블레이드, 하부 블레이드 및 상하 블레이드 추력을 중첩한 결과를 보여주고 있다. 상부 블레이드의 평균 추력이 더 높으며, 전체 평균 추력에서 약 62% 비중을 보였다. 반면 하부 블레이드의 경우는 전체 추력의 약 38% 수준을 나타내며, 동체에 근접한 하부 블레이드의 간섭 섭동 영향이 더 크게 발생함을 확인할 수 있다.

Fig. 12. Unsteady thrust variation with respect to time of the Ka-32 helicopter (hovering condition)

Download Original Figure

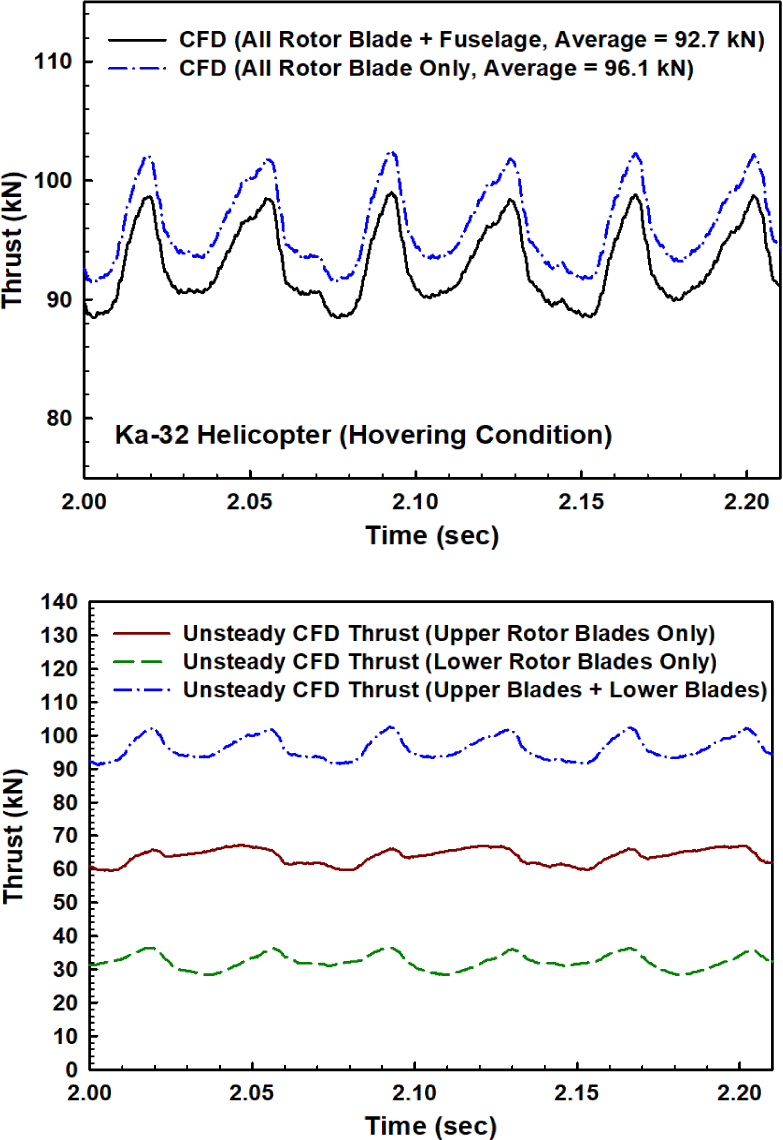
Table 2는 비행시험 시 기체 중량 대비 비정상 CFD 해석으로 구한 추력을 비교한 결과이다. CFD 해석의 추력이 동체 무게 대비 4.86% 높은 수준을 보이나, 비행시험 조건과 상당히 유사함을 확인할 수 있다. CFD 해석으로 구해진 추력이 약간 큰 이유는 본 해석에서는 방위각에 따른 블레이드의 피치각 변화는 고려하였으나, 블레이드의 공력탄성학적 변형 효과는 아직 고려하지 않았기 때문으로 판단된다. Ka-32 헬리콥터 블레이드의 구조 모델링을 위한 상세 설계 데이터가 아직 미확보 상태이기 때문에 이에 대한 영향을 고려한 해석은 향후 추가 연구가 필요한 부분이다.

전진 비행 조건(forward flight)의 경우, 블레이드 회전속도는 272rpm (28.484rad/s)이고, 속도는 148.8km/h (41.3m/s) 이다. 앞서 언급한 바와 같이 Ka-32 헬리콥터의 로터 회전축은 동체 수직축 방향에 대해 전방으로 -4.5˚ 기울어진 상태로 장착되어 있으며, 비행시험 당시 FDR에 기록된 동체의 평균 피치 각도는 약 -1.1°이다. 따라서 전진 비행시험 조건에서 평균 로터 회전면은 전방으로 약 -5.6˚ 기울어진 상태가 된다. Table 1에 제시된 전진비행 시 동체의 자세각은 초기 격자 생성 시 반영하였고, 전진 비행 조건에 해당하는 각각의 블레이드 개별 운동을 실시간으로 반영하여 비정상 유동해석을 수행하였다. 유동해석 시간 간격은 앞서와 동일하게 time-step 당 0.5˚(Δωt=0.5 deg) 회전 조건을 부가하였다.

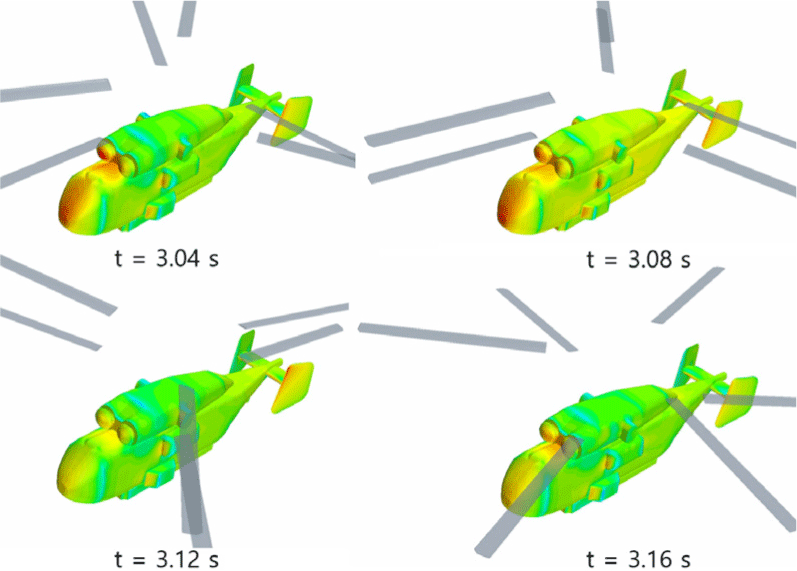
전진 비행 시 특정 시점에서 동체와 로터 주변의 와류 강도 분포를 Fig. 13에 나타내었다. 전진 속도로 인해 블레이드 끝단에서 발생한 소용돌이(vortex)가 로터 후방으로 빠르게 흘러 지나가는 모습을 볼 수 있으며, 뭉툭한 동체 형상으로 인해 발생하는 와류 강도가 제자리 비행에 비해 심하게 증가했음을 확인할 수 있다. Fig. 14는 전진 비행 시 동체 표면에 유발되는 비정상 순간 압력분포를 보여주고 있는데, 동체 상부 면에서 제자리 비행과는 달리 블레이드 내리 흐름의 영향이 전반적으로 축소되었음을 확인할 수 있다. 하지만 동체 앞쪽 전면부 경사면 영역은 블레이드가 인접한 위치에 놓일 때 여전히 상대적으로 높은 압력 수준을 나타내는 특성이 관찰되었다.

Fig. 13. Instantaneous vorticity contour on the symmetric plane of the fuselage under a forward flight condition

Download Original Figure

Fig. 14. Pressure contours on the fuselage surface of the Ka-32 helicopter at different time-steps (forward flight condition)

Download Original Figure

전진 비행 시 비정상 CFD 해석을 통해 얻은 수렴된 z-방향 공력하중(Fz)의 변화를 Fig. 15에 나타내었다. 전진 비행의 경우, 시간에 따른 추력 변화를 살펴보면 제자리 비행과 달리, 로터만의 추력과 동체를 포함한 평균 추력의 차이가 약 0.65%로 거의 동일함을 확인할 수 있다. 이는 추력 관점에서 전진 비행 시 블레이드와 동체 간의 상호 간섭 영향이 거의 없음을 의미한다. 또한 전진 비행 시 z-방향 로터 비정상 공력하중의 섭동 진폭이 38 kN(88 kN∼126 kN)을 나타내고 있다. 이는 제자리 비행 시의 약 10 kN 수준(Fig. 12)보다 현저하게 높아졌음을 확인할 수 있는데, 이런 이유로 기체에 발생하는 진동 수준이 더 증가하게 된다. 본 연구의 결과에서와 같이 정교한 CFD 해석을 통해 구해진 시간영역 동적하중은 기체 자체의 진동해석뿐만 아니라, 탑재장비에 대한 전산 진동안전성 평가 등(Kim et al., 2007)에 유용하게 활용될 수 있다.

Fig. 15. Unsteady thrust variation of the Ka-32 helicopter in a forward level flight condition (V_F=148.8 km/h)

Download Original Figure

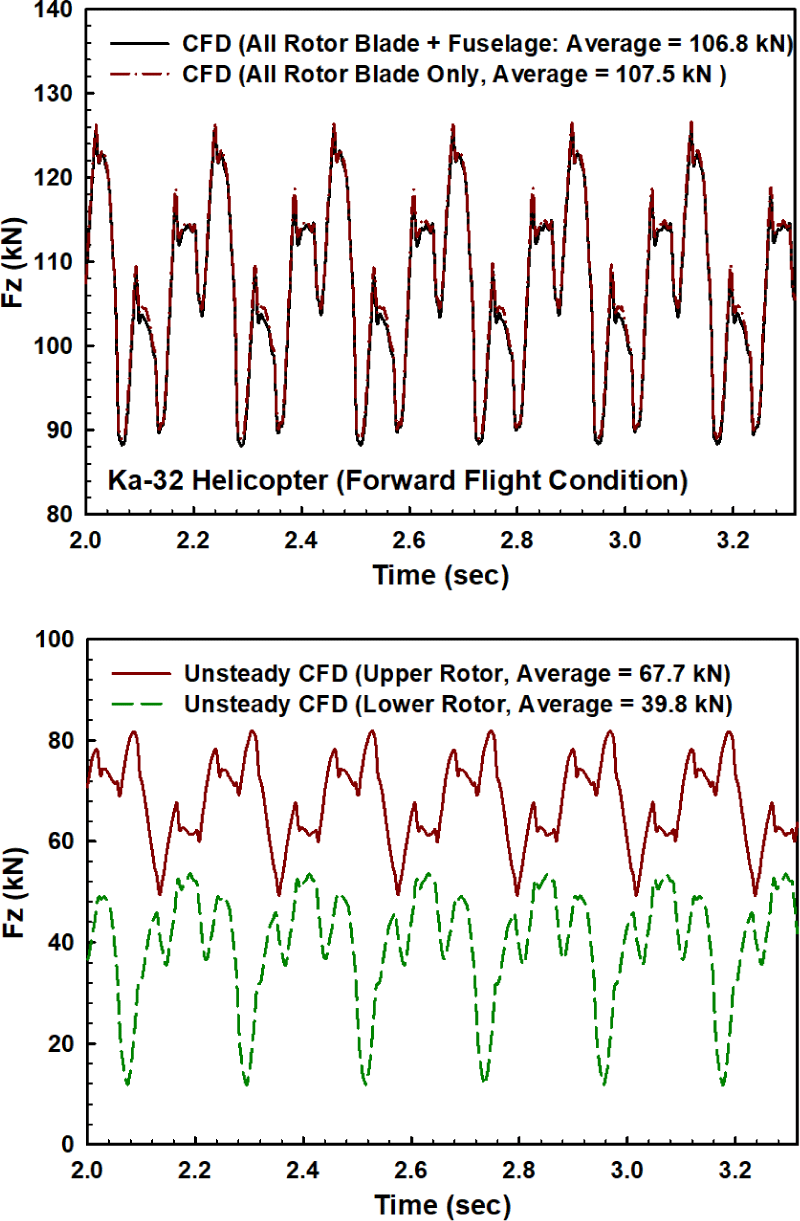
제자리 비행 조건 결과에 해당하는 Fig. 12를 비교해 볼 때 추력 섭동이 더욱 크게 발생하고 있음을 확인할 수 있다. 상부 블레이드의 평균 추력은 67.7kN이며, 하부 블레이드의 평균 추력은 39.8kN으로, 전체 평균 추력 107.5kN 대비 상부 블레이드가 차지하는 비중은 약 63%, 하부 블레이드는 약 37%로, 이는 제자리 비행 시의 추력 분담 비율은 거의 유사하다. 참고로 모든 로터 블레이드에 작용하는 수평 방향 Fx 평균 공력 하중은 -5.71kN, 동체에 작용하는 수평 방향 Fx 공력하중(항력)은 3.04kN으로 두 값의 편차는 -2.67kN이며, CFD 해석에서는 전진 추력이 항력보다 더 큰 결과가 도출되었다. 이의 원인은 현재 CFD 해석 모델에서는 매우 복잡하고 다양한 허브 부품 형상들과 엔진 흡입구 유동 등의 효과에 기인한 성분이 현재 해석 모델에서는 반영되지 않았기 때문으로 판단된다.

Ⅳ. 결 론

이 논문에서는 동축반전 로터 헬리콥터(Kamov Ka-32) 형상을 대상으로 로터의 회전 및 동적 운동과 동체 간섭 현상을 고려한 전산유체역학(CFD) 해석을 수행하고, 비행시험 데이터와 비교 및 분석하였다. CFD 해석은 제자리 비행 및 전진 비행시험 조건에서 수행되었으며, 상하 블레이드와 동체 간섭에 기인한 추력 섭동 특성을 고찰하였다. 전산유체역학 기법으로 예측한 동축반전 로터의 평균 추력은 비행시험 데이터와 비교적 잘 일치하는 결과를 보였다. 아울러 상하 로터의 추력 분담 비율은 제자리 비행의 경우 62:38, 전진 비행의 경우는 63:37 수준으로, 두 경우 모두 유사한 비율을 보였다. 또한 상하 블레이드가 발생시키는 개별 추력의 섭동 관점에서 볼 때, 전진 비행 조건에서 더 큰 경향을 보이나, 상하 블레이드 추력을 중첩한 경우에는 유사한 섭동 수준임을 파악할 수 있었다. 이 연구를 통해 동체형상을 포함한 동축반전 로터 헬리콥터에 대한 CFD 해석의 신뢰성을 부분적으로 평가하였으며, 향후 관련 설계 등에 유용한 활용이 기대된다.