중·상층 항공난류 예측모델의 성능 평가와 개선

본 연구에서 사용한 관측자료는 2019년 1월부터 2021년 12월까지의 총 3년간 민간 항공기로부터 IATA에 수집된 고도 10,000 ft 이상의 중·상층에서 한반도 영역(30~40 °N, 120~135 °E)의 in-situ EDR 관측자료를 사용하였다. 중강도 이상(Moderate-Or- Greater, MOG) 난류강도를 선별하기 위한 EDR 임계값은 선행연구(Sharman et al., 2014; Sharman and Pearson, 2017; Lee and Chun, 2018)를 참고하여 0.22 m^2/3s^-1 이상인 경우를 MOG로 설정하고 0.22 m^2/3s^-1 미만인 경우를 NIL(null)로 설정하였다.

IATA EDR 관측자료 수는 총 198,429 개로 NIL이 191,572 개(98.33%), MOG가 3,257 개(1.67%)이었다. 연도별 관측자료 수는 2019년(31,745 개) < 2020년(59,744 개) < 2021년(103,340 개) 순으로 연도가 지남에 따라 관측된 자료가 약 2배씩 증가하였다(Fig. 1a). IATA는 2017년부터 Turbulence Aware 프로그램을 구축하기 시작하면서(The IATA Turbulence Aware project, IATA, 2020), 항공 난류 관측자료를 본격적으로 수집하기 시작하였다. 이후 점차 참여 항공사가 많아져, 현재는 대한항공을 포함한 총 15개의 항공사가 실시간으로 항공난류 정보를 제공하고 있다. 이에, 한반도 상공의 난류를 관측할 수 있는 항공기가 많아지면서, COVID19 팬데믹으로 항공기 운항 수가 감소하는 시기임에도 불구하고 연도가 지남에 따라 항공 난류의 관측자료 수는 증가한 것으로 판단된다.

Fig. 1. Number of observed IATA EDR data by intensity in each year (a). MOG was shown in black and NIL was shown in gray, and number (black bar plot) and percentage (gray line plot) of observed IATA EDR data with moderate-or-greater (MOG) intensity in each year (b)

Download Original Figure

연도별 MOG 난류의 관측자료 수는 2019년에 635 개, 2020년에 985 개, 2021년에 1,637 개로 관측자료 수가 증가함에 따라 증가하였다. 하지만, MOG 관측 비율은 연도에 따라 2.00%, 1.65%, 1.58%로 감소하였다(Fig. 1b). 대기 중 CAT 발생량이 점진적으로 증가하고 있음에도 불구하고(Storer et al., 2017; Williams, 2017; Lee et al., 2019; Tenenbaum et al., 2022), 연도가 지남에 따라 MOG 난류 관측자료 비율이 감소하는 이유는 지속적인 항공 난류의 탐지 기술 향상과 예측 모델의 개발 및 개선으로부터 비롯된 것으로 보인다(Lee et al., 2022; Sharman and Pearson, 2017; Kim et al., 2009; Sharman et al., 2006). 즉, 조종사가 항공난류 의심 지역을 과거에 비하여 잘 피해 운항함으로써 MOG 난류의 관측자료 수가 해마다 줄어들고 있는 것으로 사료된다.

월별 관측자료 수는 전체적으로 봄-여름철에 많았으며, 특히 5월에 가장 많이 관측되었다. 반면, 1~2월에는 약 4,000회 이하로 관측이 보고되었다(Fig. 2). 월별 MOG 비율 또한 대체로 봄-여름철에 높아, 관측자료 수와 경향성이 유사하게 나타났다. 2019년에는 12월에 3.4%(127 개)로 MOG 비율이 가장 높았으며, 2020년에 3.1%(348 개)로 5월에 높았고, 2021년은 8월에 2.8%(327 개)로 MOG 비율이 높았다(Fig. 2).

Fig. 2. Number of observed IATA EDR data (bar plot) and percentage of MOG intensity (dash line plot) per month from 2019 to 2021. The color is different for each year (red: 2019, green: 2020, blue: 2021)

Download Original Figure

KTG는 한반도에 최적화된 한국형 중·상층 항공 난류 예측 시스템으로 동아시아 영역에 대해 개발되었다(Kim and Chun, 2011). 자세한 산출과정은 Kim and Chun(2011, 2012a)에 다뤄지고 있으며, 본 논문에서는 간략하게 기술하였다. 먼저, 기상청 현업모델을 이용하여 각 20 개의 개별난류 진단지수들에 대해 모든 격자점에서 MOG 강도에서의 AUC(Area Under Curve)를 각각 계산한다. 그리고 관측된 PIREPs의 시간 및 위치와 가장 가까운 모델 격자점에서 계산된 개별난류 진단지수들의 값을 관측된 난류 강도별[null(NIL), light(LGT), moderate(MOD), severe(SEV), extreme(EXT)]로 분류하여 임계값에 대한 look-up table을 만든다. 그 후, 누적 평균을 구하여 그 값들을 각 지수들의 난류강도에 대응되는 임계값(T1, T2, T3, T4, T5)으로 정의하고, 이를 각각 0, 0.25, 0.5, 0.75, 1의 값으로 대응시킨 1차원 매핑(mapping) 함수를 이용하여 개별지수들을 모두 0에서 1사이의 값으로 변환시켜 난류강도 예측값을 산출한다. 여기서, KTG 예측모델의 난류강도 임계치는 LGT, MOD, SEV가 각각 0.3, 0.475, 0.75로 제시되었다. 현재 KTG는 동아시아 영역에 대하여 하루 4회(00, 06, 12, 18 UTC) 3시간 간격의 30시간 예측자료가 5,000∼40,000 ft에서 5,000 ft 간격으로 제공되고 있다.

KTG는 기상청 현업 통합모델(Unified Model, UM)의 지역 예보모델(Regional Data Assimilation and Prediction System, RDAPS)을 기반으로 개발되었지만, 2019년 4월 이후로는 RDAPS 운영이 종료되면서 UM 전지구 예보모델(Global Data Assimilation Prediction System, GDAPS) 기반으로 KTG가 운영되고 있다. 따라서, 본 연구에서는 2019년 1월부터 3월까지의 KTG 예측자료는 검증에서 제외되었고, GDAPS 기반의 KTG 예측자료(2019년 4월~2021년 12월)가 검증에 사용되었다.

GKTG는 미국 국립기상연구소(National Center for Atmospheric Research, NCAR)에서 개발한 GTG3(Graphic Turbulence Guidance version3) 시스템 방법론(Sharman and Pearson, 2017)을 기반으로 개발되었으며, 17 km UM-GDAPS 자료와 항공난류 관측자료를 이용하여 개발되었다(Lee and Chun, 2018). 산출과정은 Lee and Chun(2018)에 구체적으로 서술되어 있으며, 여기서는 간략히 기술하였다. GDAPS에서 산출된 기상변수들을 이용하여 저층(지표∼10,000 ft), 중층(10,000∼20,000 ft), 상층(20,000∼50,000 ft)별로 CAT 진단지수 및 MWT 진단지수들의 확률밀도함수를 계산한다. 계산된 값의 범위 및 단위가 다른 개별난류 진단지수들을 공통의 EDR 규모로 표준화한 후, 결합하여 하나의 통합난류 예측지수인 GKTG를 산출한다. 그리하여 GKTG는 전지구 영역에 대해서 CAT와 MWT 그리고 각 격자점에서 두 난류 예측값 중 더 큰 난류강도를 반영한 MAX를 지상으로부터 41,000 ft까지 1,000 ft 간격의 고도별 수평 바람자료를 계산하여 산출하고 있다.

이후, UM-GDAPS가 10 km 해상도로 향상되어 기존 개발된 GKTG 방법론에 그대로 적용하여 개선되었다. 2019년부터 하루 4회(00, 06, 12, 18 UTC) 36시간 예측자료를 3시간 간격으로 10 km 해상도의 항공난류 예측자료가 제공되고 있다. 여기서, GKTG 예측모델의 EDR 강도 임계치는 LGT, MOD, SEV가 각각 0.15, 0.22, 0.34 m^2/3s^-1로 제시되었다.

GKTG는 3가지의 난류(CAT, MWT, MAX)를 생산하지만, 관측된 자료에서 난류의 종류를 구분할 수 없으므로 검증 시에는 모든 경우를 포함한 MAX 자료를 이용하여 검증을 진행하였다.

항공난류 정확도 검증에 사용한 통계적 검증 방법은 POD(Probability Of Detection) 방법(Mason, 1982)을 사용하였다. 이 방법은 MOG가 관측된 지점에서 난류를 예측할 확률인 POD “yes”(PODY)와 NIL이 관측된 지점에서 난류를 예측 안 할 확률 POD “no”(PODN)을 고려하여 검증하는 방법으로(Table 1, Eq. 1~2), PODY(PODN)는 MOG(NIL)이 관측된 지역과 가장 근접한 격자점에서 난류 예측값이 주어진 임의의 임계값을 넘는(넘지 않는) 경우를 셈하여 구한다(Kim and Chun, 2012a; Lee and Chun, 2018).

여기서, TP는 True Positive, FP는 False Positive, FN은 False Negative, TN은 True Negative를 나타낸다.

POD 계산을 특정 임계값에 대하여 수행하면, 한 쌍의 PODY-POFD(Probability Of False Detection)가 산출된다(Table 1, Eq. 1~3). 여기서 임계값을 변경시켜가며 POD 계산을 수행할 경우, PODY-POFD 쌍의 집합이 얻어진다. 이를 x-y 도면에 표시하여 점들을 따라 그리면 ROC(Receiver Operating Characteristic) 커브가 만들어지며, 이 곡선의 아래 면적(Area Under Curve, AUC)이 모델의 예측성을 나타내는 값이 된다(Fielding and Bell, 1997). 이에 더하여, 일기예보의 정확성 평가에 많이 사용되어온 True Skill Statistic(TSS) 방법(Allouche et al., 2006)을 이용하여 모델의 정확도 검증을 진행하였다(Eq. 4). AUC는 0.5에서 1사이의 범위를, TSS는 –1에서 +1사이의 범위의 값을 가지며 두 값 모두 1에 가까울수록 항공난류 사례들을 모두 완벽하게 예측하는 것을 의미한다. 반면, AUC는 0.5, TSS는 0에 가까울수록 예측성능이 거의 없고 무작위 추측과 동일한 예측성능을 갖는 것으로 해석할 수 있다.

예측자료는 00UTC에 생산된 10,000ft 이상의 한반도 영역(30~40°N, 120~135°E) 항공난류 예측자료를 사용하였다. 항공난류의 관측자료가 매시 모든 위경도에 대해 존재하지 않으므로, 예보중심의 검증이 아닌 관측중심의 검증을 수행하였다. 즉, 관측된 EDR값과 가장 가까운 시간과 격자점의 항공난류 예측모델 EDR값을 비교하였다. GKTG 예측값은 EDR로 변환되어 있기 때문에 관측 EDR값과 예측 EDR값의 MOG 임계값을 둘 다 0.22m^2/3s^-1이상인 경우로 셈하여 PODY와 PODN을 구하였다. 한편, KTG는 예측값이 EDR로 변환이 되어 있지 않기 때문에, 관측된 EDR이 0.22m^2/3s^-1 이상일 때, 난류강도 예측자료값이 0.475 이상(미만)인 경우를 TP(FP)으로, 관측된 EDR이 0.22m^2/3s^-1 미만일 때, 난류 강도 예측자료값이 0.475이상(미만)인 경우를 FN(TN)으로 셈하여 PODY와 PODN을 구하였다.

본 절에서는 2019~2021년(3년) 동안 전체기간, 연도별, 계절별, 그리고 월별로 관측자료와 예측자료(KTG, GKTG)간의 PODY와 PODN 및 AUC와 TSS의 통계적 검증 방법을 이용하여 항공난류 예측결과를 비교 검증하였다. 이에 더하여, 고도 및 선행시간(Lead Time)별 분석도 같이 진행하였다.

2.5.1 전체기간 및 연도별 분석

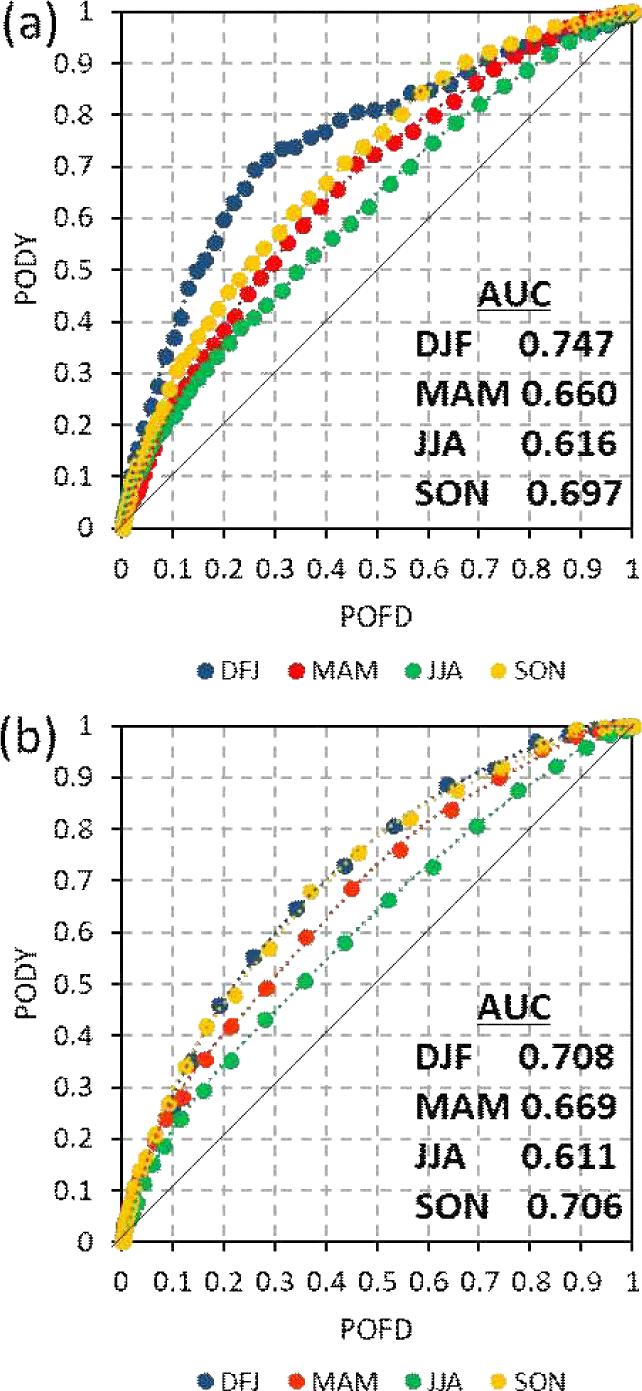
2019~2021년의 전체기간 동안 KTG의 PODY와 PODN은 각각 0.46, 0.75이었고(Tables 2~3). GKTG의 PODY와 PODN은 각각 0.22와 0.91이었다(Tables 4~5). PODY는 KTG가 0.24 높았으며, PODN은 GKTG가 0.16 높았다. TSS는 KTG와 GKTG가 각각 0.21과 0.13으로, KTG가 GKTG에 비하여 0.07 더 좋은 성능을 보였다. Aircraft Meteorological Data Relay (AMDAR) 관측자료를 활용하여 전지구 중상층 항공난류 예측모델을 검증한 Lee et al.(2022)와 비교하면(Table 6), 본 연구의 KTG PODY가 약 0.2 이상 높았으며, PODN은 약 0.22가량 낮았고 TSS는 유사했다. 그리고 GKTG는 PODY=0.22~0.23, PODN=0.96~0.97로, 본 연구결과와 유사했으며, TSS는 0.06 낮았다. AUC는 KTG와 GKTG가 각각 0.650과 0.643으로, KTG가 약간 더 좋은 성능을 보였으나 거의 비슷하였다(Fig. 3d, Table 6). 선행연구에서 in-situ EDR을 이용하여 동아시아 영역을 검증했을 때(Table 6), KTG는 0.79, 17 km-GKTG는 0.77이었다(Lee and Chun, 2018). 또한, 전지구 영역을 검증했을 때, KTG가 0.716~0.838, GKTG는 0.745~ 0.842이었다(Table 6)(Lee et al., 2022). 본 연구의 AUC는 선행연구의 AUC에 비하여 약 0.06~0.20 낮았다.

Table 2. Monthly KTG PODY by year (2019-2021) and for the entire period

Month	2019	2020	2021	Total
1	-	0.62	0.79	0.67
2	-	0.33	0.92	0.89
3	-	0.75	0.68	0.69
4	0.38	0.62	0.58	0.54
5	0.69	0.52	0.47	0.50
6	0.57	0.63	0.39	0.51
7	0.39	0.31	0.13	0.23
8	0.27	0.06	0.31	0.26
9	0.20	0.42	0.28	0.29
10	0.78	0.62	0.59	0.68
11	0.36	0.54	0.61	0.52
12	0.76	0.87	0.57	0.73
Total	0.51	0.49	0.42	0.46

Download Excel Table

Table 3. Monthly KTG PODN by year (2019-2021) and for the entire period

Month	2019	2020	2021	Total
1	-	0.60	0.60	0.60
2	-	0.67	0.59	0.61
3	-	0.68	0.73	0.72
4	0.63	0.70	0.71	0.69
5	0.69	0.72	0.66	0.69
6	0.66	0.74	0.76	0.73
7	0.87	0.76	0.90	0.84
8	0.91	0.90	0.81	0.85
9	0.89	0.78	0.83	0.82
10	0.71	0.75	0.85	0.79
11	0.70	0.81	0.75	0.76
12	0.63	0.73	0.70	0.69
Total	0.74	0.75	0.75	0.75

Download Excel Table

Table 4. Monthly GKTG PODY by year (2019-2021) and for the entire period

Month	2019	2020	2021	Total
1	0.55	0.17	0.55	0.31
2	1.00	0.00	0.60	0.58
3	0.85	0.38	0.44	0.49
4	0.24	0.28	0.21	0.23
5	0.23	0.21	0.33	0.27
6	0.36	0.41	0.12	0.26
7	0.02	0.08	0.04	0.05
8	0.05	0.01	0.16	0.12
9	0.04	0.24	0.11	0.12
10	0.40	0.13	0.30	0.30
11	0.04	0.38	0.33	0.25
12	0.28	0.53	0.24	0.29
Total	0.22	0.22	0.22	0.22

Download Excel Table

Table 5. Monthly GKTG PODN by year (2019-2021) and for the entire period

Month	2019	2020	2021	Total
1	0.87	0.88	0.78	0.83
2	0.83	0.92	0.78	0.81
3	0.76	0.91	0.88	0.88
4	0.88	0.93	0.91	0.91
5	0.92	0.91	0.82	0.87
6	0.87	0.90	0.94	0.92
7	0.97	0.92	0.98	0.96
8	0.97	0.97	0.94	0.95
9	0.97	0.94	0.97	0.96
10	0.90	0.94	0.96	0.94
11	0.93	0.93	0.88	0.90
12	0.89	0.91	0.89	0.90
Total	0.92	0.92	0.90	0.91

Download Excel Table

Table 6. Reference table of turbulence model verification by observation (in-situ EDR)

NWP(res,)	Domain	PODY	PODN	TSS	AUC	ref.
GTG3
-	USA	-	-	-	0.825	Wandishin et al. (2014)
-	Global region	0.20	0.99	0.19	0.868	Lee et al.(2022)
KTG
RDAPS(12km)	East Asia	-	-	0.40	0.790	Lee et al.(2022)
RDAPS(12km)	Global region	0.22	0.98	0.21	0.838	Lee et al.(2022)
GDAPS(12km)	Korea	0.46	0.75	0.21	0.650	This study
GKTG
GDAPS(17km)	East Asia	-	-	0.33	0.770	Lee et al.(2018)
GDAPS(17km)	Global region	-	-	0.37	0.790	Lee et al.(2018)
GDAPS(10km)	Global region	0.22	0.97	0.19	0.842	Lee et al.(2022)
GDAPS(10km)	Korea	0.22	0.91	0.13	0.643	This study

There appear turbulence model, input numerical weather prediction (NWP), area of verification, PODY, PODN, TSS, AUC, verification period and reference.

Download Excel Table

Fig. 3. ROC curve of KTG and GKTG by year ((a) 2019, (b) 2020, (c) 2021 and (d) total)

Download Original Figure

전체적으로, 두 항공난류 예측모델 비교에서는 GKTG보다 KTG의 성능이 좋았다. 그리고MOG 난류강도를 예측할 성능이 높은 모델은 KTG이었으며, NIL을 예측할 성능이 높은 모델은 GKTG이었다. 이러한 결과는 KTG의 난류강도 임계값이 한반도에 최적화되어 있는 반면, GKTG의 난류강도 임계값은 한반도에 최적화되어있지 않고 GTG 예측모델의 임계값으로 설정되어있다. 이에 GKTG의 예측성능이 비교적 낮았던 것으로 판단된다.

실제로 항공산업에 종사하는 관제사나 항공운항관리사 등이 유용하게 활용하기 위한 신뢰도 높은 예측모델의 AUC 값은 일반적으로 최소 0.8 이상으로 알려져 있는데(Kim et al., 2009), 본 연구에서 두 모델의 AUC 값은 이에 미치지 못하였다. 한편, 같은 10 km-GDAPS 자료를 초기 입력자료로 사용하는 Lee et al.(2022)의 GKTG AUC는 0.842로 높았다(Table 6). 같은 초기 입력자료를 사용하고 있음에도 불구하고 AUC가 다른 이유는 항공기상청에서 사용하는 KTG 및 GKTG는 입력되는 초기모델 및 해상도 변경에 따라 난류 진단지수들을 재산출하고 표준화하는 최적화가 이루어지지 않았으나, Lee et al.(2022)의 GKTG는 10 km-GDAPS에 맞추어 난류 진단지수들을 최적화하여 적용하였기 때문이다. 즉, 본 연구의 항공난류 예측모델에 대한 난류 진단지수들의 최적화가 이루어지지 않았기 때문에, AUC가 0.8에 미치지 못했던 것으로 판단된다.

연도별로 살펴보면, KTG의 PODN은 3년 동안 0.74~0.75에서 나타나 차이가 거의 없었지만, PODY는 2019년에서 2021년으로 연도가 지남에 따라 각각 0.51, 0.49, 0.42로 낮아졌다(Tables 2~3). 반면, GKTG의 PODY와 PODN은 각각 0.22, 0.90~0.92 범위에서 변동하여 3년이 유사했다(Tables 4~5). TSS는 KTG와 GKTG가 각각 2019년에 0.25, 0.14, 2020년에 0.24, 0.14, 2021년에 0.17, 0.13이었으며, 두 모델 모두 연도가 지남에 따라 TSS가 낮아졌다. KTG의 AUC는 2019년(0.666), 2020년(0.663), 2021년(0.636) 순으로, GKTG의 AUC는 2020년(0.658), 2019년(0.648), 2021(0.633) 순으로 높았으며, 두 모델 모두 2021년에 가장 낮았다(Fig. 3). 이러한 결과는 선행연구에서 보고한 KTG의 AUC 값(0.739~0.821)보다 낮았으며(Kim and Chun, 2011, 2012a; Lee et al., 2022), GKTG의 AUC 값(0.745~0.842)도 선행연구에 비해 낮았다(Lee et al., 2022).

두 모델 모두 2019년과 2020년의 예측성능이 유사했고 2021년에는 비교적 낮았는데, 이처럼 연도별로 예측모델 성능이 다른 것은 선행연구에서도 나타났다. Kim et al.(2009)은 가장 좋은 예측성을 보이는 GTG 시스템의 난류 진단지수들이 해마다 다름을 확인하였으며, 한반도 상공의 CAT 발생 메커니즘이 매년 상이함을 보고하였다. 따라서, 동일한 모델임에도 불구하고 연도별로 성능이 조금씩 달랐던 것으로 판단된다.

2.5.2 계절 및 월별 분석

계절별 KTG와 GKTG의 PODY, PODN과 TSS는 Table 7에 나타내었고 ROC 커브와 AUC는 Fig. 4에 나타내었다. 두 모델 모두 PODY는 겨울철이 가장 높았으며, 다음으로 봄, 가을, 여름 순으로 높았다(Table 7). PODN은 여름, 가을, 봄, 겨울 순으로 높았다. TSS는 PODY와 동일한 경향성을 보였다. 그리고 KTG와 GKTG를 비교하면 모든 계절에서 KTG의 TSS가 높았다. 계절별 AUC를 살펴보면(Fig. 4), 두 모델 모두 겨울, 가을, 봄, 여름 순으로 높았으며, 겨울과 가을에는 AUC가 약 0.7을 보였다. 또한, 겨울과 여름에는 KTG가 더 높았고 봄과 가을은 GKTG가 더 높았다. 선행연구에서 PIREPs를 이용하여 검증한 AUC 결과도 가을(0.800∼0.807)과 겨울(0.790∼0.847)에 높고 여름(0.783∼0.790)에 가장 낮아 본 연구와 유사한 경향성을 보였다(Kim and Chun, 2011, 2012a). 이렇게 계절별로 성능이 다르다는 것은 한반도 상공의 항공난류가 발생하는 원인이 계절별로 다른 메커니즘을 가지고 있음을 의미한다.

Table 7. Seasonal PODY, PODN and TSS of KTG and GKTG over 3 years

	KTG			GKTG
	PODY	PODN	TSS	PODY	PODN	TSS
Winter (DJF)	0.74	0.66	0.40	0.35	0.86	0.22
Spring (MAM)	0.52	0.70	0.22	0.28	0.88	0.16
Summer (JJA)	0.34	0.81	0.15	0.15	0.94	0.09
Autumn (SON)	0.46	0.79	0.25	0.21	0.94	0.14
Total	0.46	0.75	0.21	0.22	0.91	0.13

Download Excel Table

Fig. 4. Seasonal ROC curve of (a) KTG and (b) GKTG over 3 years

Download Original Figure

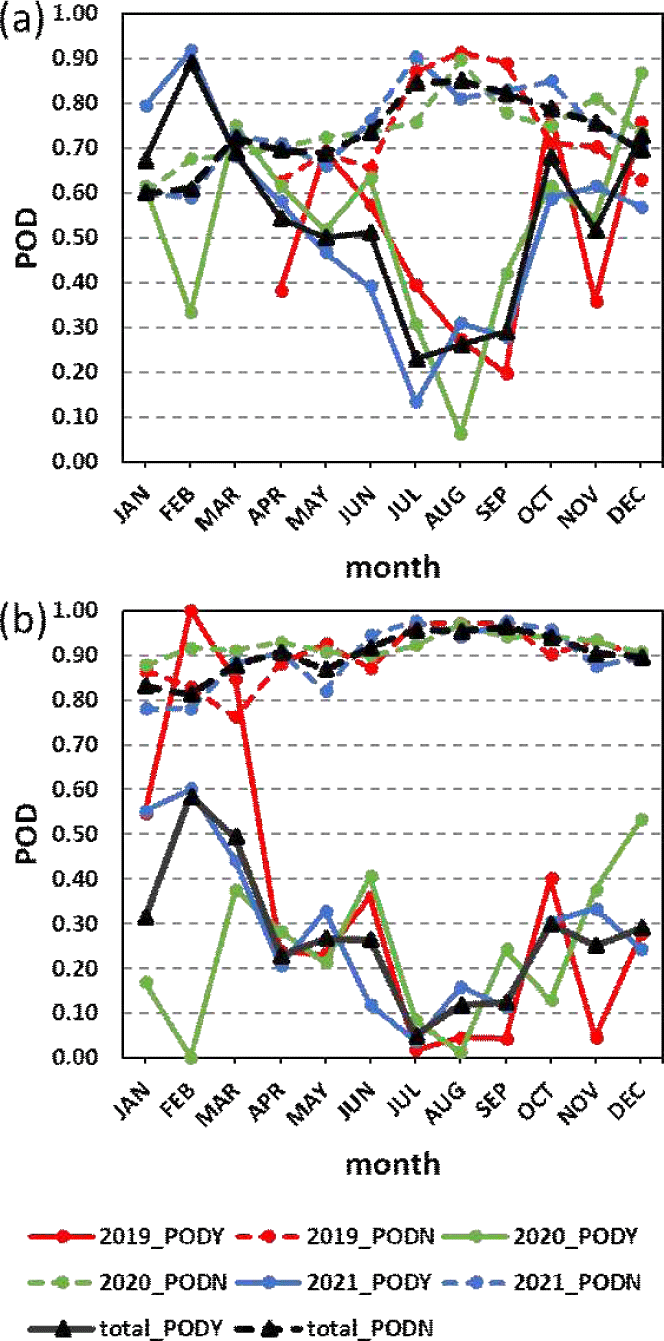
더 나아가, KTG와 GKTG의 월별 변동성을 살펴보면(Tables 2~5, Fig. 5), 전체적으로 두 모델 모두 10~3월에 PODY가 높고 PODN이 낮은 경향성을 보였다. 7~9월에는 PODY는 KTG와 GKTG 각각 약 0.3, 0.15 이하로 급격히 낮아지고 PODN이 높은 경향성을 보였다. 이는 7~8월에 장마와 태풍과 같은 대류 시스템이(Lee and Chun, 2015; Kim et al., 2009; Kim and Chun, 2011), 9월에는 대류성 구름이 발달하면서 발생하는 대류유도난류(Convectively Induced Turbulence, CIT)가 주요 원인으로 항공난류를 발생시키기 때문에(Lee and Chun, 2015), 7~9월의 정확도가 확연히 떨어진 것으로 보인다. 그리고 1~2월에는 연도에 따라 PODY의 차이가 컸는데, 이는 1~2월에 관측자료 수가 적어서 산출시에 영향을 준 것으로 판단된다.

Fig. 5. PODY and PODN of (a) KTG and (b) GKTG by year (red: 2019, green: 2020, blue: 2021) and for the entire period

Download Original Figure

3년 전체기간에 대한 TSS 월별 분석을 수행한 결과를 Table 8에 나타내었다. 전체적으로 GKTG보다 KTG의 TSS가 높게 나타났다. KTG는 2, 3, 10, 12월에 TSS가 0.40 이상으로 높았으며, GKTG는 2, 3월에 각각 0.40, 0.37로 높았다. 또한 앞서 설명한 PODY 및 AUC와 마찬가지로 여름철에는 낮은 정확도를 보였다. Lee et al.(2022)의 전지구 항공난류 검증연구와 비교하면, KTG는 0.166~0.225로 본 연구와 유사하게 나타났으나, GKTG는 0.19로 본 연구의 TSS가 0.06 낮았다.

Table 8. Monthly TSS for the entire period of KTG and GKTG

Month	KTG	GKTG
1	0.27	0.15
2	0.50	0.40
3	0.41	0.37
4	0.24	0.14
5	0.19	0.14
6	0.24	0.18
7	0.07	0.01
8	0.11	0.07
9	0.11	0.09
10	0.47	0.24
11	0.27	0.16
12	0.42	0.19
Total	0.21	0.13

Download Excel Table

정리하면, 월별 KTG와 GKTG의 예측성능은 공통적으로 가을-겨울철에 높고 봄-여름철에 비교적 낮은 경향성이 보이며, 이러한 경향성은 선행연구에서도 보고되었다(Lee and Chun, 2015; Kim et al., 2009; Kim and Chun, 2011). 또한, 검증 시 대류에 의한 난류, 구름 주변 난류 등에 의한 관측자료를 분류하여 검증을 진행하지 못했기 때문에 봄-여름철의 정확도가 낮아졌을 가능성이 있다. 즉, KTG와 GKTG가 중강도 이상의 CAT 및 MWT를 가을-겨울철에 가장 잘 예측하는 반면, 대류 시스템이 활발한 여름철에는 거의 모의를 못 하거나, 난류 원인을 분류하지 못하여 정확도가 낮았던 것으로 판단된다.

2.5.4 선행시간별 분석

검증에 사용된 00 UTC의 3시간 간격 24시간 예측에 대해서 선행시간별 정확도 분석을 진행하여 Fig. 6에 나타내었다. 검증에 사용된 항공난류 예측자료의 선행시간 중 가장 빈번하게 사용된 선행시간은 3~9시 예측자료이며, 선행시간이 지남에 따라 관측자료 수는 반 이상으로 감소하였다. PODY는 선행시간이 지남에 따라 낮아지는 경향을 보였다. KTG와 GKTG 모두 15~18시 예측시간에 높았다. 반면, PODN은 선행시간이 지남에 따라 높아졌으며, 두 모델 모두 21~24시 예측시간에 가장 높았다. TSS도 PODN과 같이 선행시간이 지남에 따라 낮아지는 경향을 보였으나, 15~18시 예측시간에 가장 높았다.

Fig. 6. PODY, PODN and TSS by lead time of (a) KTG and (b) GKTG for each year (2019~2021) and the entire period

Download Original Figure

2019년에는 특이하게 KTG에서 선행시간이 지남에 따라 PODY와 TSS가 크게 튀는 부분이 존재하였다. 이는 관측자료 수와 관련이 있는 것으로 보인다. 전반적으로 선행시간별로 관측자료 수는 1600개 이상, MOG 관측자료 수는 20개 이상 존재한다. 반면, 2019년의 튀는 선행시간(15, 21시) 관측자료 수는 1,000개 이하이며, MOG 관측자료 수는 20개 이하로 매우 적었다. 즉, 1년의 관측자료만으로 항공난류를 검증하는 것은 검증자료 수가 적기 때문에 검증 시 오류를 범할 가능성이 높았다. 이에 다년간의 관측자료를 이용함으로써 더욱 신뢰성 높은 검증이 가능한 것으로 판단된다.

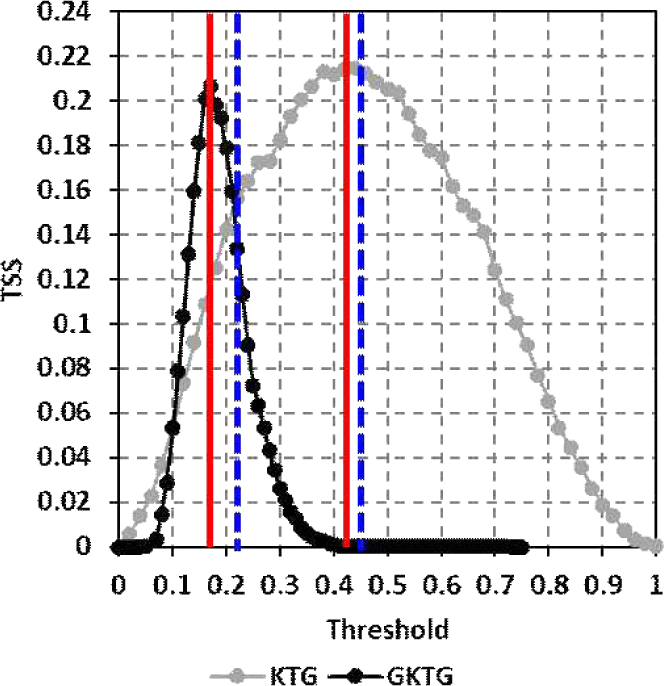
위의 검증을 통하여 KTG와 GKTG의 성능 수준을 객관적으로 살펴보았다. 모델을 개선하는 방법은 다양하지만, 본 연구에서는 한 가지 간단한 개선 방법을 제시하고자 한다. 이는 in-situ EDR 난류 관측자료와 항공난류 모델예측 자료를 비교하여 최적의 난류강도 예측 임계값을 다시 부여하는 방법이다. 객관적인 최적의 난류강도 예측 임계값을 산출하는 방법은 다음과 같다. 먼저 MOG 난류 관측자료에 대하여 임의의 간격으로 모델의 임계값을 변경시켜가며 TSS를 구한다. 다음으로, TSS가 가장 높은 임계값으로 최적의 난류강도 예측 임계값을 다시 부여하는 방법이다. 본 연구에서는 임계값을 0.01 간격으로 변경시키며 TSS를 산출하였다.

이 방법으로 산출한 KTG와 GKTG의 임계값별 TSS를 Fig. 7에 나타내었다. KTG는 기존 임계값(0.475)과 최적 임계값(0.44)의 TSS가 각각 0.210과 0.214로 차이가 없었다. 반면, GKTG는 기존 임계값(0.22)과 최적 임계값(0.17)의 TSS가 각각 0.134와 0.207로, 기존 임계값에서 최적 임계값으로 변경하면 모델의 정확도가 많이 개선될 수 있음을 확인하였다. 하지만, 모델 자체의 성능이 좋아진 것은 아니기 때문에 추후에 실질적인 모델의 개선이 필요하다.

Fig. 7. TSS according to threshold of KTG and GKTG. The blue dotted line marked the existing threshold and the red solid line marked improved threshold

Download Original Figure